International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1350
ISSN 2229-5518
R. Rajkhowa
Abstract: We explain particular, unique, approximate solutions of the Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) evolution equations and also solutions of DGLAP evolution equations by using regge behaviour of structure functions and method of characteristic for t and x-evolutions of singlet and non-singlet structure functions in leading order (LO) and next-to-leading order (NLO). Hence t-evolution of deuteron, proton, neutron and difference of proton and neutron and x-evolution of deuteron, proton and neutron structure functions in LO and NLO at low-x from DGLAP evolution equations. The results of t and x-evolutions are compared with experimental data and global parameterization in different kinematics region. We also compare the solutions of DGLAP evolution equations among themselves.
equation, Structure function, Low-x physics.
¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯![]() ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯
¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯
Among different evolution equations, up till now
Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) [1-4]
evolution equations are most successful and major tools to
experimental data in different kinematics region. We also compare the solutions of DGLAP evolution equations among themselves.
IJSER
study the structure functions of hadrons and ultimately
structure of matter, ultrahigh-energy cosmic rays. Various
methods, like particular, unique, approximate,
characteristic, regge and brute-force, Laguerre-polynomial, Mellin-transformation etc. methods have been developed for the analytical and numerical solution. In this paper, we are concentrate our work mainly in different analytical
Though the necessary theory has been discussed elsewhere [5-13], here we mention some essential steps for clarity. The DGLAP evolution equations with splitting functions [14-16] for singlet and non-singlet structure functions in LO and NLO are in the standard forms [5-13,
17]
solutions of DGLAP evolution equations in leading order
(LO), next-to-leading order (NLO) and compare them
∂F S ( x, t )
![]()
∂t
α ′ (t )
![]()
−
2π
particularly by focusing on the numerical accuracy,
approximation and better fitness of results with experimental data and global parameterization in different![]()
[ 2 {3 + 4 ln(1 −
3
1
x)} S ( x, t) +
2
4 1 dw![]()
![]()
3 ∫ 1 − w
{(1 +
w 2 )
![]()
F S x
w
, t − 2
F S ( x, t)}]
2
kinematics region.![]()
+ n ∫ {w2 + (1 − w) 2 }G( x , t )dw}] = 0,
(1)
Here, we explain particular, unique, approximate solutions of the DGLAP evolution equations and also solutions of DGLAP evolution equations by using regge
behaviour of structure functions and method of
f x
∂F NS ( x, t )
![]()
∂t
2
![]()
− α s′ (t )
2π
![]()
NS
w
![]()
4 1 dw
NS x NS
characteristic for t and x-evolutions of singlet and non-
singlet structure functions in leading order (LO) and next-
[ 3 {3 + 4 ln(1 − x)} F 2
(x, t) +
3 ∫ 1 − w
{(1 + w2 )F2
, t − 2F
w
(x, t)}] = 0,
(2)
to-leading order (NLO). Hence t-evolution of deuteron,
for LO. And
proton, neutron, difference of proton and neutron and x-
∂F S ( x, t)
α (t )
evolution of deuteron and proton structure functions in LO
and NLO at low-x from DGLAP evolution equations. The
2 − s
∂t 2π
[ 2 {3 + 4 ln(1 − x)}F
( x, t) + 4 1 dw {(1 + w )F
x , t
2F ( x, t)}![]()
results of t and x-evolutions are compared with
3![]()
•Author is currently working as a assistant professor at T. 1
S
2 3 ∫ 1 − w
x
![]()
![]()
![]()
2 S − S
2 w 2
H. B. College, Jamugurihat, Sonitpur, Assam, India, Pin-![]()
+ n ∫{w2 + (1 − w)2}G(
f x w
, t)dw}]
784180. E-mail: rasna.rajkhowa@gmail.com, phone no. :
α s (t) 2 S 1
1 S x
+919854492326![]()
−
![]()
[(x − 1)F2 ( x, t) ∫ f (w)dw + ∫ f (w)F2 (
, t)dw
2π
0 x w
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1351
ISSN 2229-5518
![]()
1 S S x![]()
1 S x
2 ( )![]()
= 182![]()
+ 14![]()
+ 40
136![]()
+ −
38 ![]()
−
− − + 2
+ ∫ Fqq (w) F2 ( w , t )dw + ∫ Fqg (w)G( w , t )dw] = 0,
Fqg w
w
9 9 9w
w ln w
3 3
4 ln(1 w)
(2 8w) ln w
x
∂F NS ( x, t )
x
![]()
α s (t )
(3)
+ − ln 2
![]()
w + 44
3![]()
ln w − 2 ln 2 (1 − w) + 4 ln(1 − w) + π
3
218 ![]()
− Pqg (w)
![]()
2 −
∂t 2π
2 NS
4 1 dw
2 NS x NS
+ 2 qg (−w)
1 /(1+ w) dz
![]()
∫ ln
w /(1+ w)
![]()
1 − z ,
z
![]()
3 {3 + 4 ln(1 − x)}F2
( x,t) + ∫ {(1 + w
3 1 − w
)F2
, t − 2F
w
( x,t)}
where, P
(w) = w2 2
x
qg +(1-w) , CA , CG , CF , and TR are constants
α s (t) 2
NS 1
1 NS x
associated with the color SU(3) group and CA = CG = NC = 3,
CF = (NC 2-1)/ 2NC and TR = 1/ 2. NC is the number of
![]()
−
π
( x − 1)F
2![]()
( x, t) ∫ f (w)dw + ∫ f (w)F
, t dw = 0
w
colours.
2
0 x
(4)
Using the variable u = 1-w and Taylor expansion
for NLO, where
β
33 − 2N
method [18-19], singlet structure function F2 S(x/w, t) and gluon structure function G(x/w, t) can be approximated for
α / (t ) = 4π ,
4π
α s (t ) =
1 − 1 ln t ,
β = f
and
small-x as![]()
s β0t
![]()
β t
β 2t 0 3
u ∂F S ( x, t )
306 − 38N
F S x
w t ≅ F S
+ 2 .
(5)
β = f ,
2 ( / , )
2 ( x, t )
x.
1 − u ∂x
![]()
1
Similarly, G(x/w, t) can be approximated for small-x as
Nf being the number of flavours. Here,
u ∂G( x, t) . (6)
f (w) = C 2 [P (w) − P (w)] + 1 C
C [P (w) + P (w)] + C T N P
(w),
G( x / w, t ) ≅ G( x, t ) + x.
1 − u ∂x![]()
![]()
![]()
![]()
IJSER
![]()
F F A
2 F A G A
F R f N F
Using equations (5) and (6) in equation (1) and performing
F S (w) = 2CF TR N f Fqq (w)
u-integrations we get
A x F S x t A
and
S ′ 1( )
2 ( , ) +
2 ( x)G( x, t )
∂F2 ( x, t )
α s (t ) =
(7)
F S (w) = CF TR
N f F1
(w) + CGTR
N f F 2 (w).
−
∂t 2π
+ A ( x)
∂F S ( x, t )
2
0.
∂G( x, t )
+ A ( x)
The explicit forms of higher order kernels are [14-16]
3 ∂x
4 ∂x
![]()
1 + w2
Where, A1 (x), A2 (x), A3 (x) and A4 (x) are some functions of x
PF (w) = −2
ln w ln(1 − w)
[5].
1 − w
![]()
![]()
3 + 2w ln w − 1 (1 + w) ln 2 w − 5(1 − w),
1 − w 2
We assume [5-13]
G(x, t) = K(x) F2 S(x, t). (8)
where K(x) is a parameter to be determined from
phenomenological analysis and we assume K(x) = K, axb or
PG (w) =
1 + w ln 2
![]()
w + 11
ln w +
=67
− =π
ce dx
where K, a, b, c and d are constants. Though we have
1 − w
3 9 3
assumed some simple standard functional forms of K(x),![]()
+ 2(1 + w) ln w + 40 (1 − w),
3
yet we can not rule out the other possibilities.
Therefore equations (7) becomes
2 1 + w2
∂F S ( x, t)
A f
∂F S ( x, t)
(9)
P (w) =
− ln w − 5 − 2(1 − w),
− L ( x)F S ( x, t) + L
( x)
= 0.
![]()
![]()
![]()
N F 3 1 − w 3
2 1/(1 w)
![]()
∂t
Here,![]()
t 1 2
![]()
2 ∂x
1 + w
+ dk
1 − k
PA (w) =
2
1 − w ![]()
![]()
ln + 2(1 + w) ln w + 4(1 − w),
k k
L ( x ) = A ( x ) + K( x )A ( x ) + A ( x ) ∂K( x ) ,
w /(1+w)
1 1 2
4 ∂x
20 56 2 8 2 2![]()
![]()
Fqq (w) = − 2 + 6w − w + 1 + 5w + w ln w − (1 + w) ln w,
![]()
9w 9 3
F1 (w) = 4 − 9w − (1 − 4w) ln w − (1 − 2w) ln 2 w + 4 ln(1 − w)
L2 (x) = A3 (x) + K(x) A4 (x)
And
Af = 4/(33-2nf ).
The general solutions [19-20] of equation (9) are
−
−
+ 2 ln2 1
w 1
− 4 ln
w 2
− π + 10 P
(w)
1 1 ![]()
w ![]()
![]()
w 3
qg![]()
U x, t, F S = t exp ∫
![]()
dx
and
2
IJSER © 2013 http://www.ijser.org
A f
L ( x)
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1352
ISSN 2229-5518
and
L x
F NS
F NS
t 2
![]()
(15)
V x, t, F S = F S ( x, t ) exp∫
![]()
1 ( ) dx.
2 = 2
( x, t0 ) ,
2 2
L2 ( x)
t 0
which give the t-evolutions of non-singlet structure
Since U and V are two independent solutions of
functions in LO. And also
equation (9) and if α and β are arbitrary constants, then V =
F NS ( x, t) = F NS (
, ) exp x 2
− =P( x) dx,
(16)
αU + β may be taken as a complete solution [19-20] of equation (9). So, the complete solution
![]()
2 2 x0 t
∫ A
0 f
Q( x)
Q( x)
L ( x)
1 L ( x)
which give the x-evolutions of non-singlet structure
F S ( x, t ) exp∫ 1 dx = αt exp ∫ 1 dx + β
(10)
functions in LO. Here,
2 L2 ( x)
A f
L2 ( x)
P( x) =
3![]()
A1( x),
Q( x) =
3
![]()
3 ( x).
is a two-parameter family of surfaces. The one parameter 2 2
family determined by taking β = α2 has equation
L x
Proceeding exactly in the same way, from equations (3)
and (4) we get
F S ( x, t ) exp
1( ) dx = αt exp 1
1 dx + α 2 .
2
∫ l x
A ∫ L
t (b / t +1)
1
1
2
2 ( )
![]()
![]()
f 2 ( x)
F S ,NS ( x, t ) = F S ,NS ( x, t
)
exp2b
− ,
(17)
2
![]()
2 0
(b / t +1)
![]()
t
![]()
t
(11)
t 0
0
Differentiating equation (11) with respect to α, we get
S S x
2 1
L1( x)
+ 0M1( x)
![]()
F2 ( x, t) = F2 ( x0 , t) exp x a . L x
−
T M x L x
![]()
dx,
T M x
α = − 1 t exp 1
∫ 1 dx.![]()
![]()
![]()
( ) +
0
2 ( )
2 ( ) + 0
( )
2 A
L ( x)
+ T
(18)
Putting the value of α in equation (11), we get
NS ( x, t ) =
F NS
2
x 2 1
![]()
![]()
( x0 , t ) exp ∫ . −
A1 ( x)
![]()
0 B1( x)
dx,
L ( x)
0 + 0
+ 0
![]()
F S ( x, t ) = − 1 t 2 exp∫ 2
![]()
− 1 dx,
(12)
x a
A3 ( x)
T B3 ( x)
A3 ( x)
T B3 ( x)
2 4
f 2 ( x) L
(19)
which gives the t and x-evolution of singlet and non-singlet
which is merely a particular solution of the general
solution. Now, defining
structure functions in NLO where a = 2/β o , b = β 1 /β 0 2. We observe that in case of t-evolutions, if b tends to zero, then
1 2![]()
1 ( x)
equation (17) tends to equation (13) and (14) respectively,
F S ( x, t
![]()
) = −
t 2 exp∫
L
− dx,
at t = t0,
i.e., solution of NLO equations goes to that of LO equations.
2 4 0
A L ( x)
L ( x)
Physically b tends to zero means number of flavours is
where, t0 = ln (Q0 2/Λ2) at any lower value Q = Q0 , we get from equation (12)
high. Here,
M1 ( x), M
( x), B ( x), B
1 2
( x) B ( x)
3
and
B4 ( x)
are
F S x t F S
t 2
![]()
(13)
some functions of x [5-7].
For all these particular solutions, taking β = α2. But if
2 ( , ) =
2 ( x, t0 ) ,
using β = α and differentiating with respect to α as before,
the value of α can not be determined. In general, if taking β
which gives the t-evolution of singlet structure function
F2 S(x, t). Again defining,
we obtain from equation (12)
= αy, in the solutions the powers of (t/t0 ) and the numerators of the first term inside the integral sign be y/(y-1) for t and![]()
x-evolutions respectively in LO. Similarly the powers of
L
F S ( x
, t ) = −
![]()
1 t 2 exp
2
1 ( x)
− dx ,
t b / t +1
b / t0 +1
0
and co-efficient of b (1/t-1/to ) of
2 4 A f
L2 ( x)
L ( x)
x = x
0
exponential part in t-evolutions and the numerators of the first term inside the integral sign be y/(y-1) for x-evolutions
x
L ( x)
in NLO. Then if y varies from minimum (=2) to maximum
S S
2
1
F ( x, t ) = F
2 2
( x0
, t ) exp ∫ A
−
L ( x) L
dx
( x)
(= ∞) then y/(y-1) varies from 2 to 1.
x0 f 2
2
(14)
Deuteron, proton and neutron structure functions [21]
can be written as
which gives the x-evolution of singlet structure function
F2 S(x, t). Proceeding in the same way, we get
F2 d(x, t) = (5/9) F 2 S(x, t), (20)
F2 p(x, t) = (5/18) F2 S(x, t) + (3/ 18) F2 NS (x, t),
(21)
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1353
ISSN 2229-5518
F2 n(x, t) = (5/18) F2 S(x, t) – (3/ 18) F2 NS (x, t).
(22)
F S ( x, t ) = αt exp∫ 1
− L1 ( x) dx.
(29)
Now using equations (13), (15) in equations (20-22) and (14)
in equation (20) one obtains the t-evolutions of deuteron,![]()
2
Now, defining![]()
L ( x)
proton, neutron and difference of proton and neutron and
x-evolution of deuteron structure functions at low-x as
F S ( x, t
) = αt
exp∫ 1
− L1 ( x) dx,
at t = t0 ,
F d , p, n ( x, t ) = F d , p, n ( x, t
t 2
) ,
(23)
2 0 0
![]()
A
f
L2 ( x)
![]()
L ( x)
2 2 0
![]()
t 0
where t
= ln (Q
/Λ ) at any lower value Q = Q , we get
0
0 2 2 0
F p (x,t) − F n (x,t) = [
p (x,t ) − F n (x,t )](
)2,
(24)
from equations (29)![]()
2 2 0 0 t
0
F S ( x, t ) =
2
t
![]()
F ( x, t )
2
(30)
x
L ( x)
t 0
d d
2
1
(25)
F ( x, t) = F
2 2
( x0 , t) exp
∫ A
− dx
L ( x) L ( x)
which gives the t-evolutions of singlet structure function
x f 2
2
F2 S
(x, t) in LO. Proceeding in the same way we get
in LO for β = α2. The corresponding results in NLO [6-7] for
S S x 1
=L ( x)
(31)
2 ( , )
2 ( 0 , ) exp
1 dx
β = α2 are
2
![]()
F x t = F x t
∫
x
−
A L ( x)
2
L ( x)
2
t (b / t +1)
F d , p,n ( x, t ) = F d , p,n ( x, t
)
exp2b 1 − =1 ,
(26)
which gives the x-evolutions of singlet structure function
2 2 0
![]()
(b / 0 +1)
![]()
t
t
F2 S(x, t) in LO. Similarly, for non-singlet structure functions
t0
0
F NS x t
F NS
t
![]()
(32)
2
2 ( , ) = 2
( x, t 0 ) t ,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
IJSER
t (b / t+1)
0
F p ( x, t) − F n ( x, t) = [F p ( x, t0 ) − F p ( x, t0 )]
exp2b 1 − 1 ,
2 2 2 2
(b / t0 +1)
t
t0
t0
NS NS
x 1
P( x)
(33)
x 2 1
L1( x) + T M1( x)
(27)
F ( x, t ) = F
2 2
( x0 , t ) exp ∫
x0
A Q( x)
−
Q( x)
dx,
![]()
F d ( x,t) = F d ( x ,t) exp ∫ .
− 0 dx ,
which give the t and x-evolutions of non-singlet structure
2 2 0
x a L ( x) + T M
( x)
L ( x) + T M
( x)
functions in LO and
0 2 0 2
2 0 2
(28)
S ,NS
S ,NS
t (b / t +1)
1
(34)
F x t = F
x t b t
b −
The determination of x-evolutions of proton and neutron
2 ( , ) 2
( , 0 ) (
t
/ 0 +1)
exp ,
t t
structure functions like that of deuteron structure function
is not suitable by this methodology; because to extract the
0
S S x 1 1
L1( x) + 0M1( x)
(35)
x-evolution of proton and neutron structure functions, we
![]()
F2 ( x, t) = F2 ( x0 , t) exp x a . L x
![]()
−
T M x L x
dx,
T M x
are to put equations (14) and (16) in equations (21) and (22).
2 ( ) + 0
2 ( )
2 ( ) + 0
( )
x 1 1
A6 ( x) + T B6 ( x) ,
But as the functions inside the integral sign of equations
F NS ( x, t) = F NS ( x , t) exp ∫ .
![]()
− 0 dx
(14) and (16) are different, two separate the input functions
2 2 0
![]()
x a
A ( x) + T B
( x)
A ( x) + T B
( x)
F2 S(x0 , t) and F 2 NS(x0 , t) are needed from the data points to
0 5 0 5
5 0 5
(36)
extract the x-evolutions of the proton and neutron structure
functions, which may contain large errors.
Due to conservation of the electromagnetic current,
which give the t and x-evolutions of singlet and non-singlet structure functions in NLO.
Therefore corresponding results for t-evolution of
deuteron, proton, neutron and difference of proton and
neutron structure functions are
F2
must vanish as Q2 goes to zero [21-22]. Since the value of Λ
F d , p, n x t
F d , p, n ( ,
) t ,
(37)
2 ( , ) = 2![]()
x t0 t
is so small we can take at Q = Λ, F2 S(x, t) = 0 due to conservation of the electromagnetic current [22]. This
p n p
0
p
t
dynamical prediction agrees with most adhoc![]()
F2 ( x, t) − F2 ( x, t) = [F2 ( x, t0 ) − F2 ( x, t0 )] ,
t
(38)
parameterizations and with the data [23]. Using this
boundary condition in equation (10) we get β = 0 and
in LO and
0
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1354
ISSN 2229-5518
t (b / t +1)
∂F S ( x, t )
![]()
∂t
S
![]()
− R1 ( x) = 0 , (45)
t
F d , p,n ( x, t) = F d , p,n ( x, t
![]()
![]()
![]()
) expb 1 − 1 ,
(39)
2 2 0
(b / 0 +1)
t
t0
where, R (x) is a some function of x [13].
t
1
Equation (45) can be solve as
t (b / t +1)
F S x t
R ( x)
= Kt
(46)![]()
F p ( x, t) − F n ( x, t) = [F p ( x, t ) − F p ( x, t )]
![]()
![]()
expb 1 − 1 ,
2 ( , ) 1 ,
2 2 2 0
2 0 (b / 0 +1)
t
t
t0
0
(40)
where K is a integration constant.
From equation (46), the t and x-evolutions of singlet
in NLO. Again x-evolution of deuteron structure function in LO and NLO respectively are
structure function in LO can be obtained as
R ( x)
S S =t 1
(47)
x
L ( x)
F2 ( x, t ) = F2 ( x, t0 ) t ,
F d ( x, t ) = F d ( x , t ) exp
1 − 1 ,
(41)
0
0 ∫ A L x L
![]()
dx
2 2
x
f 2 ( )
2 ( x)
R ( x)−R ( x )
0
F S ( x, t ) = F S ( x
, t )t 1
1 0 . (48)
L x + T
2 2 0
d d x
1 1
1( ) 0M1( x)
Proceeding in the same way, t and x-evolutions of non-![]()
F2 ( x,t) = F2 ( x0 ,t) exp x a . L x
−
T M x L x
dx.
T M x
( ) +
0
2 ( )
2 ( ) + 0
( )
(42)
singlet structure function in LO can be obtained as
t 2 ( x)
(49)
NS NS x
![]()
F2 ( x, t ) = F2
( 0 , t )
Already we have mentioned that the determination of x-
evolutions of proton and neutron structure functions like
that of deuteron structure function is not suitable by this
NS ( x, t ) = F NS
t0
( x0 , t ) t
{ 2 ( x)
− 2 ( x
)} . (50)
methodology. It is to be noted that unique solutions of
where, R2 ( x) is a some function of x [13].
evolution equations of difIferent Jstructure fuSnctions are ER
same with particular solutions for maximum y (y = ∞) in β =
αy relation.
The t and x-evolution of singlet and non-singlet
structure functions corresponding to NLO are respectively
R
S S
3( x)
, (51)![]()
F2 ( x, t ) = F2 ( x, t 0 ) t
It is to be noted that approximate solution of DGLAP
evolution equation is obtained by considering αU + βV = 0
0
t
R ( x)
4
F NS ( x, t ) = F NS ( x, t
)
, (52)
instead of V = αU + β in equation (10) and the results [9-12] 2![]()
2 0 t 0
are same with the result of unique solutions.
R ( x)−R ( x
F S ( x, t ) = F S ( x
, t )t 3
3 0 , (53)
2 2 0
R
( x)−R ( x
)
Using the Regge behaviour of singlet and non-singlet
F NS ( x, t ) = F NS ( x
, t ) t 4
4 0 , (54)
structure functions [12-13] as
2 2 0
F S ( x, t ) = T (t ) x − λ S and
F NS ( x, t ) = T
− λ
(t ) x NS ,
where,
R3 ( x) and R4 ( x) are some functions of x [13].
2 1 2 2
F S ω
Now using equations (47), (49) and (48), (50) in
singlet structure functions
2 ( x /
, t )
and non-singlet
equations (20), (21) and (22), the t and x-evolutions of
structure function F S ( x / ω, t ) can be approximated as
2
deuteron, proton and neutron structure functions at low-x
can be obtained as
F S x ω t = T
ωλ S − λ S
= F S ωλ
(43)
R ( x)
2 ( / , )
1(t ) x
2 ( x, t ) S ,
d d =t 1
(55)
F2 ( x, t ) = F2 ( x, t 0 ) t
F NS
2
( x / ω, t ) =
F NS
2
( x, t )ω
λ
NS ,
(44)
0
R ( x)−R ( x
d d 1
1 0 , (56)
where T1 (t) and T2 (t) are functions of t, and λS and λNS are
the Regge intercepts for singlet and non-singlet structure
F2 ( x, t ) = F2 ( x0 , t )t
R ( x)
2( x)
functions respectively.
F P ( x, t ) = F P ( x, t
) 5t 1
+ 3t ,
(57)
Using Regge behaviour of structure function and the relation between gluon and singlet structure function
2 2 0
5t0
![]()
R ( x)
1
+ 3t0
2( x)
(equation (8)) in equation (1) one obtains the following
P P 5t
R ( x)
1
+ 3t
R ( x)
2
form of equation![]()
F2 ( x, t ) = F2
( x0 , t )
R ( x )
R ( x ) ,
(58)
5t 1
0 + 3t 2 0
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1355
ISSN 2229-5518
S S t
A f L1(x)
R ( x)
3 2( x)
F2 ( x, t ) = F2 ( x, t0 )
. (71)
R
n n 5t 1 − t
![]()
t0
![]()
F2 ( x, t ) = F2 ( x, t0 )
R ( x)
R ( x) ,
(59)
x
5t0 1
− 3t0 2
L ( x)
![]()
F S ( x, t ) = F S ( x , t ) exp− ∫ 1 dx . (72)
and
2 2 0
x0 L2 ( x)
R ( x)
3 2( x)
Proceeding in the same way, t and x evolutions of non-
R
n n 5t 1 − t
![]()
F2 ( x, t ) = F2 ( x0 , t )
R ( x )
R ( x ) .
(60)
singlet structure function can be obtained as
5t 1
0 − 3t 2 0
NS NS
A (x)
t
in LO. The corresponding results in NLO are
F2 ( x, t ) = F2
![]()
( x, t0 )
, (73)
d = d
R ( x)
3
, (61)
t0
F2 ( x, t )
![]()
F2 ( x, t 0 ) t
x
0
F NS
( x, t ) = F NS
( x , t ) exp − ∫
A1 ( x) dx
. (74)
R ( x)−R ( x
)
2 2 0
( x)
x
F d ( x, t ) = F d ( x
, t ) t 3
3 0 , (62)
0
2 2 0
R ( x)
5t 3 + 3t
R ( x)
4
Now using equations (71) and (72) in equations (20), t and
x-evolution of deuteron structure functions in LO can be
P P , (63)
F2 ( x, t ) = F2
( x, t0 )
5t0
R ( x
3
) + 3t
R ( x)
4
obtained as
d d
A f
L1 ( x)
, (75)
R R F
![]()
x t = F
![]()
P P 5t
3( x) + 3t
4 ( x)
(64)
2 ( , )
2 ( x, t0 ) t
F2 ( x, t ) = F2 ( x0 , t )
R ( x )
R ( x ) ,
0
5t 3
R
0 + 3t 4 0
R
d d
x L1 ( x)
, (76)
5t 3( x) − 3t
4 ( x)
F ( x, t ) = F
( x , t ) exp−
∫ dx![]()
IJSER
n n , (65)
2 2 0
L2 ( x)
![]()
F2 ( x, t) = F2 ( x, t0 )
5t
R ( x
3
) − 3t
R ( x) x
4
0 0 The corresponding results in NLO are
and
R R 3 A
L ( x) + T M
( x)
n n 5t
![]()
3( x) − 3t
4 ( x)
F d ( x, t )
F d ( x, t
)
f 1
0 1
, (77)
F2 ( x, t ) = F2 ( x0 , t )
R ( x )
R ( x ) .
(66)
2 = 2
![]()
0 t
5t 3
0 − 3t 4 0
0
It is to be noted that Taylor series expansion method can
d ( , )
d ( , ) exp
x L ( x) + T
0
M1( x)
, (78)
not be used to solve DGLAP evolution equations in regge
F x t = F
2 2
x0 t
![]()
− ∫
L ( x) + T M
dx
( x)
behaviour of structure functions. Since in regge behavior,
region of discussion is at very low-x, so boundary condition
x0 2
0 2
F2 (x, t) at x =1 also can not be used.
For method of characteristics, two new variables S and τ
used instead of x and t [8] in equation (10), such that![]()
dt = −t , (67)
dS
dx
Since the equation (71) and (73) as well as (72) and (74) are
not in the same form, so two separate the input functions
F2 S(x0 , t) and F 2 NS(x0 , t) are needed from the data points to extract the t and x-evolution of proton and neutron structure function. So using equations (21) and (22), determination of evolutions of proton and neutron structure functions is not possible. In all the methods, for possible solutions in NLO, an extra assumption [7, 11]
![]()
= A f L2 ( x)
dS
(68)
2
α s (t )
α s (t )
is to be introduced, where T0 is![]()
= T
![]()
= T T
Therefore equation (10) can be written as
S
2π
0 2π 0 1
α (t )
dF2 (S,τ ) + L (S,τ )F S (S,τ ) = 0 . (69)
a numerical parameter and T
= s . By a suitable choice
![]()
dS 1 2
1 2π
Solution of equation (69) is
L ( S ,τ)
t
of T0 we can reduce the error to a minimum.
S S
![]()
F2 (S,τ ) = F2 (τ )
, (70)
t0
where L1 (S, τ) = A f .L1 (x) and F2 S(S, τ) = F2 S (τ); S = 0, t = t0 . After changing the variable (S and τ) to the original variable (x and t), the t and x-evolution of singlet structure function in LO [8] can be obtained as
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1356
ISSN 2229-5518
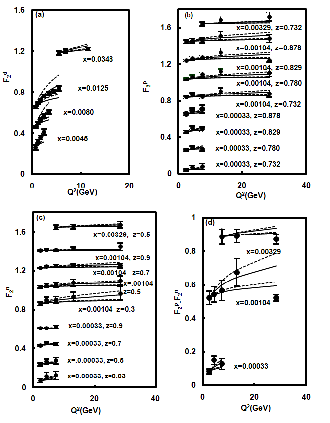
αy relation in NLO. Data points at lowest-Q2 values in the figures are taken as input to test the evolution equation.
Fig.1 (a-d): Results of t-evolutions of deuteron, proton, neutron and difference of proton and neutron structure functions (dashed lines for LO and solid lines for NLO) for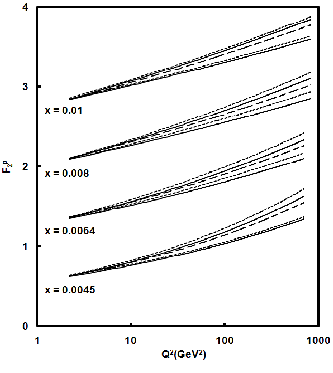
Fig.2: Results of t-evolutions of proton structure functions F2 p (dashed lines for LO and solid lines for NLO) with recent global paramatrization (long dashed lines) for the
the representative values of x in LO and NLO for NMC
data. For convenience, value of each data point is increased by adding 0.2i, where i = 0, 1, 2, 3 ... are the numberings of curves counting from the bottom of the lowermost curve as the 0-th order. Data points at lowest-Q2 values in the figures are taken as input.
Results of particular solutions [5-7] of t-evolution of deuteron, proton, neutron and difference of proton and neutron structure functions compared with the NMC [25] and HERA [26] low-x and low-Q2 data and results of x- evolution of deuteron structure functions with NMC low-x and low-Q2 data. In case of HERA data, proton and neutron structure functions are measured in the range 2 ≤ Q2 ≤ 50
GeV2. Moreover, here PT ≤ 200 MeV, where PT is the
transverse momentum of the final state baryon. In case of NMC data, proton and neutron structure functions are measured in the range 0.75 ≤ Q2 ≤ 27 GeV2. We consider number of flavours nf = 4.
In fig.1(a-d), represents results of t-evolutions of
deuteron, proton, neutron and difference of proton and neutron structure functions (solid lines) for the representative values of x given in the figures for y = 2 (upper solid lines) and y maximum (lower solid lines) in β =
representative values of x given in the figures. Data points at lowest-Q2 values in the figures are taken as input. For convenience, value of each data point is increased by adding 0.5i, where i = 0, 1, 2, 3, ... are the numberings of curves counting from the bottom of the lowermost curve as the 0- th order.
Agreement with the data [25-26] is good. The same figures, represents the results of t-evolutions of deuteron, proton, neutron and difference of proton and neutron structure functions (dashed lines) for the particular solutions in LO. Here, upper dashed lines for y = 2 and lower dashed lines for y maximum in β = αy relation. We observe that t-evolutions are slightly steeper in LO calculations than those
of NLO. But differences in results for proton and neutron structure functions are smaller and NLO results for y = 2 are of better agreement with experimental data in general.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1357
ISSN 2229-5518
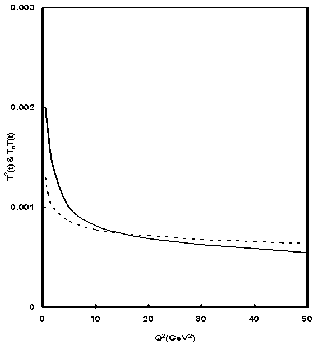
Fig.3: T(t)2 and T0 T(t), where T(t) = αs (t)/2π against Q2 in the Q2 range 0 ≤ Q2 ≤ 50 GeV2.
In fig.2, we compare our results of t-evolutions of proton
structure functions F2 p (solid lines) with recent global
parameterization [27] (long dashed lines) for the representative values of x given in the figures for y = 2 (upper solid lines) and y maximum (lower solid lines) in β = αy relation in NLO. Data points at lowest-Q2 values in the figures are taken as input to test the evolution equation. In the same figure, we also plot the results of t-evolutions of proton structure functions F 2 p (dashed lines) for the particular solutions in LO. Here, upper dashed lines for y =
2 and lower dashed lines for y maximum in β = αy relation. We observe that t-evolutions are slightly steeper in LO calculations than those of NLO. Agreement with the NLO results is found to be better than with the LO results.
Unique and approximate solutions of t-evolution for
structure functions are same with particular solutions for y
maximum (y = ∞) in β = αy relation in LO and NLO.
In fig.3, we plot T(t)2 and T0 T(t), where T(t) = αs (t)/2π against Q2 in the Q2 range 0 ≤ Q2≤ 50 GeV2 as required by our data used. Though the explicit value of T0 is not necessary in calculating t- evolution of, yet we observe that for T0 = 0.108, errors become minimum in the Q2 range 0 ≤ Q2≤ 50 GeV2.
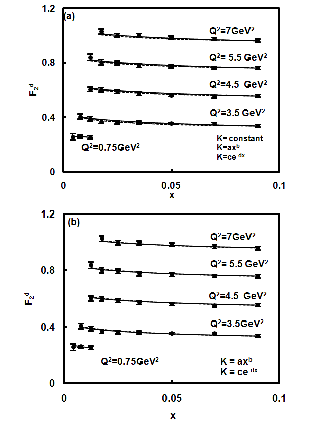
Fig. 4(a-b): Results of x-distribution of deuteron
structure functions F2 d in LO for K(x) = k (constant) (solid lines), K(x) = axb (dashed lines) and for K(x) = ce- dx (dotted lines), where k = 4.5, a = 4.5, b = 0.01, c = 5, b = 1 and in NLO for K(x) = axb (solid lines), and for K(x) = ce- dx (dotted lines), where a = 5.5, b = 0.016, c = 0.28, and d = -3.8 and for representative values of Q2 given in each figure, and compare them with NMC deuteron low-x low-Q2 data. In each the data point for x-value just below 0. 1 has been taken as input F2 d (x0 , t). For convenience, value of each data point is increased by adding 0.2i, where i = 0, 1, 2, 3, ... are the numberings of curves counting from the bottom of the lowermost curve as the 0-th order.
In figs.4 (a-b), represents results of x-distribution of deuteron structure functions F2 d in LO (fig. 4(a)) for K(x) = k (constant) (solid lines), K(x) = axb (dashed lines) and for K(x)
= ce-dx (dotted lines), and in NLO (fig.4(b)) for K(x) = axb (solid lines) and for K(x) = ce-dx (dashed lines) where a, b, c and d are constants and for representative values of Q2 given in each figure , and compare them with NMC deuteron low-x low-Q2 data [25]. In each data point for x- value just below 0.1 has been taken as input F2 d (x 0 , t). In case of LO, agreement of the results with experimental data is good at k = 4.5, a= 4.5, b = 0.01, c = 5, d = 1. For x- evolutions of deuteron structure function, results of unique solutions and results of particular solutions have not any
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1358
ISSN 2229-5518
significance difference in LO [6]. In case of NLO, agreement of the result with experimental data is found to be excellent at a =10, b = 0.016, c = 0.5, d =-3.8 for y minimum (y = 2) and a
=5.5, b = 0.016, c = 0.28, d =-3.8 for y maximum (y = ∞) in
relation β=αy. But agreement of the results with experimental data is found to be very poor for any constant value of k. Therefore we do not present our result at K(x) = k in NLO.
Though the results of regge behavior has been discussed elsewhere [13], here we mention some important point.
Nature of results of t and x- evolution of structure
functions is same with the results of particular solutions and agreement of the result with experimental data and global parameterization is good. In all the result from experimental as well as global fits, it is seen that structure functions increases when x decreases and Q2 increases for fixed values of Q2 and x respectively. But the results of t and x- evolution of structure functions are not unique which depend on various parameters K(x), λS , λNS in LO
The evolution results are discussed in section-3(a) for the particular, unique and approximate methods. Particular and unique solutions of singlet and non-singlet structure functions at low-x are obtain using by Taylor’s expansion method from GLDAP evolution equations and derive t- evolution for deuteron, proton, neutron and difference of proton and neutron structure functions and x-evolutions of deuteron structure functions and compare them with global data and parameterizations with satisfactory phenomenological success. Particular solutions of DGLAP evolution equations in LO and NLO obtained by that methodology were not unique and so the t- evolutions of deuteron, proton and neutron structure functions, and x- evolution of deuteron structure function obtained by this methodology were not unique. Thus by this methodology, instead of having a single solution we arrive a band of solutions, of course the range for these solutions is reasonably narrow.
In case of unique solutions, it has been observed that though we have derived a unique t-evolution for deuteron, proton, neutron, difference and ratio of proton and neutron
IJSER
and K(x), λS , λNS and T0 in NLO.
K(x) comes from the relation between gluon and singlet
structure function, which is a function of x. Here also taking some simple standard functional forms of K(x) which are same with the particular solutions i.e., K(x)= k, axb, and cedx. Explicit form of K(x) can actually be obtained only by solving coupled DGLAP evolution equations for singlet and gluon structure functions considering regge behaviour. λS and λNS are regge intercepts for singlet and non-singlet structure functions and T0 is a numerical parameter.
It is observed that result is sensitive to arbitrary parameters k, a, b, c, d and λS , λNS , T0 in t and x-evolutions.
Nature of results [8] of characteristic method for t and x- evolution of structure functions is same with the results of particular solutions and agreement of the result with experimental data and global parameterization is good. In all the result from experimental as well as global fits, it is seen that structure functions increases when x decreases and Q2 increases for fixed values of Q2 and x respectively. But the results of t and x- evolution of structure functions are not unique which depend on parameters K(x) in LO and K(x) and T0 in NLO.
Here also taking some simple standard functional forms
of K(x) which are same with the particular solutions i.e.,
K(x)= k, axb, and cedx. T0 is a numerical parameter.
It is observed that result is sensitive to arbitrary parameters k, a, b, c, d and T0 in t and x-evolutions.
structure functions in LO and NLO, yet we can not
establish a completely unique x-evolution for deuteron
structure function in LO and NLO due to the relation K(x) between singlet and gluon structure functions and an adhoc parameter T 0 in NLO. This parameter does not effect in the results of t- evolution of structure functions. K(x) may be in the forms of a constant, an exponential function or a power function and they can equally produce required x- distribution of deuteron structure functions. But unlike many parameter arbitrary input x-distribution functions generally used in the literature, these methods require only one or two such parameters. Unique solutions are obtain using by boundary condition, structure function F2 = 0 at x
=1. Unique and approximate solutions of t and x-evolution
for structure functions are same with particular solutions
for y maximum (y = ∞) in β = αy relation in LO and NLO. In all the result from experimental as well as global fits, it is seen that deuteron structure functions increases when x decreases and Q2 increases for fixed values of Q2 and x respectively, and proton, neutron, difference of proton and neutron structure functions increases when Q2 increases for fixed value of x.
It is to be noted that the determination of x- evolutions of proton and neutron structure functions like that of deuteron structure function is not suitable by this methodology; because to extract the x-evolution of proton and neutron structure functions, two separate singlet input function F2 S(x0 , t) and non-singlet input functions F2 NS(x0 , t) are needed from the data points to extract the x-evolutions
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1359
ISSN 2229-5518
of the proton and neutron structure functions, which may contain large errors.
The evolution results are discussed in section-3(b) for the Regge behavior of structure functions. DGLAP evolution equations in LO and NLO have solved by considering Regge behavior of singlet and non-singlet structure functions at low-x and derive t and x-evolutions of various structure functions. It has been observed that t and x-evolutions for deuteron, proton and neutron structure functions in LO and NLO are not unique due to the relation K(x) between singlet and gluon structure functions, Regge intercept λS , λNS and an adhoc parameter T0 in NLO. Where λS and λNS are the Regge intercepts for singlet and non-singlet structure functions respectively. K(x) may be in the forms of a constant, an exponential function or a power function and they can equally produce required t and x-distribution of proton and deuteron structure functions. Explicit form of K(x) can actually be obtained only by solving coupled DGLAP evolution equations for singlet and gluon structure functions considering regge behaviuor of structure functions [13]. On the other hand, we observed that the Taylor expansion method can not be used to solve DGLAP evolution equations considering regge behavior of structure functions. In all the result from experimental as well as global fits, it is seen that deuteron and proton structure functions increases when x decreases and Q2 increases for fixed values of Q2 and x respectively.
The evolution results are discussed in section-3(c) for
the characteristic method. The solutions of singlet and non- singlet structure functions at low-x are obtained by using method of characteristic from GLDAP evolution equations and derive t and x-evolutions of deuteron structure functions. It has been observed that t and x-evolution for deuteron structure functions in LO and NLO are not unique due to the relation K(x) between singlet and gluon structure functions and an adhoc parameter T0 in NLO. K(x) may be in the forms of a constant, an exponential function or a power function and they can equally produce required t and x-distribution of deuteron structure functions. In this method, boundary condition F2 S(S, τ) = F 2 S (τ); t = t0 , x = τ at S = 0 is used to obtain the solution. On the other hand, we observed that the Taylor expansion method can be used to solve DGLAP evolution equations in this method. In all the result from experimental as well as global fits, it is seen that deuteron and proton structure functions increases when x decreases and Q2 increases for fixed values of Q2 and x respectively.
It is to be noted that the determination of t and x-
evolutions of proton and neutron structure functions like that of deuteron structure function is not suitable by this methodology; because to extract the t and x-evolution of
proton and neutron structure functions, two separate singlet input function F2 S(x0 , t) and non-singlet input
functions F2 NS(x0 , t) are needed from the data points to extract the x-evolutions of the proton and neutron structure functions, which may contain large errors.
Comparisons of these methods are summarized in
Table-1.
Table-1
Summary of Comparisons of these evolution methods.
is not suitable by this methodology.
5. For possible solutions of DGLAP
evolution equations in NLO, we introduce an adhoc numerical parameter T0 , which does not effect the results of t- evolution of structure functions.
6. Explicit form of K(x) can not be obtained
by solving coupled DGLAP evolution
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1360

ISSN 2229-5518
structure functions.
5. Explicit form of K(x) can not be obtained
by solving coupled DGLAP evolution equations for singlet and gluon structure
functions by this methodology.
7. Boundary condition [F2 S(S, τ) = F 2 S (τ); t
= t0 , x = τ at S = 0.] is used to solve the
DGLAP evolution equations.
[1] G Altarelli and G Parisi, Nucl. Phys B 126 (1977) 298.
[2] G Altarelli, Phy. Rep. 81 (1981) 1.
[3] V Gribov and L Lipatov, Sov. J. Nucl. Phys. 15 (1972) 438
& 675.
[4] Y L Dokshitzer, Sov. Phys. JETP 46 (1977) 641.
[5] R Rajkhowa and J K Sarma, Indian J. Phys. 78(9) (2004)
979.
[6] R Rajkhowa and J K Sarma, Indian J. Phys., 78A (3) (2004) 367.
[7] R Rajkhowa and J K Sarma, Indian J. Phys. 79(1) (2005)
55.
SER
3. The determination of x-evolutions of deuteron, proton and neutron structure
functions is suitable by this methodology.
4. For possible solutions of DGLAP evolution equations in NLO, we introduce an adhoc numerical parameter T0 , which effects the results of t and x-evolution of
[8] R. Baishya, R. Rajkhowa and J K Sarma, J. Assam Sc.
Soc., Vol.46, 44-51(2005). R. Baishya and
J K Sarma, Physical ReviewD 74, 107702 (2006)
[9] J K Sarma, D K Choudhury, G K Medhi, Phys. Lett.
[10] J K Sarma and G A Ahmed, Indian Journal of Pure & Applied Physics, 40 (2002) 235.
[11] A Deshamukhya and D K Choudhury, Indian J. Phys.
[12] J. K. Sarma, G. K. Medhi, Eur. Phys. J. C 16 (2000) 481. [13] U. Jamil and J.K. Sarma, Pramana, Journal of Physics,
Regge Behaviour and Spin-independent and Spin- dependent Structure Functions, Ph. D. Thesis, T.U. (2008) (Private Communication).
[14] W Furmanski and R Petronzio, Nucl. Phys. B 195 (1982)
237.
[15] W Furmanski and R Petronzio, Z. Phys. C11 (1982)
293.
[16] W Furmanski and R Petronzio, Phys. Lett B 97 (1980)
437.
[17] L F Abbott, W B Atwood and R M Barnett, Phys. Rev.
[18] I S Granshteyn and I M Ryzhik, ‘Tables of Integrals, Series and Products’, ed. Alen Jeffrey, Academic Press, New York (1965).
[19] F Ayres Jr, ‘Differential Equations’, Schaum's Outline
Series, McGraw-Hill (1988).
[20] F H Miller, ‘Partial Differential Equation’, John and
Willey (1960).
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1361
ISSN 2229-5518
[21] F Halzen and A D Martin, ‘Quarks and Lepton, An
Introductory Course in Modern Particle Physics’, John
Wiley and Sons, New York (1990).
[22] B Badelek et. al, ‘Small-x Physics’, DESY 91-124,
October (1991).
[23] E Reya, ‘Perturbative Quantum Chromodynamics’,
DESY 79/88, DO-TH 79/20 (1979).
[24] J B Scarborough, ‘Numerical Mathematical Analysis’, Oxford & IBH Publishing Co. Pvt. Ltd. (1966).
[25] M Arneodo, hep-ex / 961031, NMC, Nucl. Phys. B 483 (1997) 3.
[26] C Adloff, H1 Collaboration, DESY 98-169, hep-
ex/9811013 (1998).
[27] A D Martin et. al, hep-ph/0110215 (2001).
IJSER
IJSER © 2013 http://www.ijser.org