International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 182

ISSN 2229-5518

Boundary Layer Flow & Heat Transfer of an

Unsteady Dusty Fluid over a Stretching Sheet

S.K.Mishra and A.K.Rauta

Abstract- The unsteady flow and heat transfer of a viscous incompressible dusty fluid over a vertical stretching sheet is studied. The governing partial differential equations are solved by reducing into ordinary differential equations using similarity transformations and the solutions have been found using well known Runge-Kutta method with help of Shooting technique. The effect of pertinent flow parameters such as Unsteady parameter, Froud number, Grashof number, Prandtl number, Eckert number, Volume fraction, fluid interaction parameter etc on heat transfer are investigated with help of tables and graphs. W e have found that our result is good agreement with previously published results. It is found that the thermal and momentum boundary layer thickness decreases on the increase of unsteady parameter and the temperature of both fluid phase as well as particle phase are enhancing on the increase of Eckert number. It is also noticed that the rate of cooling is faster for higher prandtl number and unsteady parameter.

AMS classification: 76T10, 76T15

Keywords:

Boundary layer flow, Eckert number, Fluid – particle interaction parameter, Froud number, Grashof number, Prandtl number, Shooting techniques, Stretching sheet, Unsteady parameter, Volume fraction.

——————————————————————————————————————————————————————————————

1. Introduction:

The unsteady flow and heat transfer of two phase viscous incompressible flow over a stretching sheet is occurring in several industrial applications and technologies. The practical applications are underground disposable of radioactive waste materials, exothermic and endothermic reactions , centrifugal separation of particles, blood rheology, flow through packed beds, sedimentation etc
.The momentum and Heat transfer in the laminar boundary layer flow on a moving surface is also important for both practical as well as theoretical point of view because of their wide application in heat removal from nuclear fuel debris, the aerodynamic extrusion of plastic sheet, glass blowing, cooling or drying of papers, drawing plastic films , extrusion of polymer melt-spinning process and heat treated materials traveling on conveyer belt etc .Due to this fact several researchers motivated to study the effect of momentum and heat transfer.
The study of the boundary layer flow over a stretched surface moving with a constant velocity was initiated by Sakiadis B.C.[18] in 1961.Then many researchers extended the above study with the effect of Heat Transfer .Tsou et.al [20] studied the effect of Heat Transfer and experimentally confirmed the numerical result of Sakiadis . Grubka et.al[9] investigated the temperature field in the flow over a stretching surface when subject to uniform heat flux
.Sharidan[19] presented similarity solutions for unsteady
boundary layer flow and heat Transfer due to stretching sheet .A numerical solution for laminar thermal boundary over a flat plate with convective surface boundary condition was analyzed by Aziz[1].Chen [6] investigated mixed convection of a power law fluid past a stretching
surface in presence of thermal radiation and magnetic field
.Crane [13] has obtained the Exponential solution for
planar viscous flow of linear stretching sheet. Chamakha
et.al.[7] Investigated the unsteady magneto hydrodynamics boundary layer flow of viscous incompressible electrical conducting fluid along a semi infinite vertical permeable plate. Nandkeolyar et.al. [16] have studied the effect of ramped surface temperature on the flow and heat transfer of a viscous, incompressible and electrically conducting dusty fluid in presence of transverse magnetic fluid,M Das et.al. [14] recently have studied the unsteady hydro magnetic flow of a Heat absorbing Dusty Fluid past a permeable vertical plate with ramped temperature. B.J. Gireesha et.al[4] have studied the effect of hydrodynamic laminar boundary layer flow and heat Transfer of a dusty fluid over an unsteady stretching surface in presence of non uniform heat source/sink .They have examined the Heat Transfer characteristics for two type of boundary conditions namely variable wall temperature and variable Heat flux. G.K.Ramesh et.al [8] have investigated the momentum and heat transfer characteristics in hydrodynamic flow of dusty fluid over an inclined stretching sheet with non uniform heat source/sink .B.G. Gireesh et.al [3] also studied the mixed convective flow a dusty fluid over a stretching sheet in presence of thermal radiation, space dependent heat source/sink.
In this paper the study of effect of different flow parameters on unsteady boundary layer and heat transfer of a dusty fluid over a stretching sheet have investigated. The problem of two phase suspension flow is solved in the

IJSER © 2015 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 183

ISSN 2229-5518

frame work of a model of a two-way coupling model or a
two-fluid approach.
Here, the particles will be allowed to diffuse through the carrier fluid i.e. the random motion of the particles shall be taken into account because of the small size of the particles. This can be done by applying the kinetic theory of gases and hence the motion of the particles across the streamline due to the concentration and pressure diffusion. We have considered the terms related to the heat added to the
system to slip-energy flux in the energy equation of particle
velocity Uw(x) along the x-axis, keeping the origin fixed in
the fluid of ambient temperature𝑇∞. Both the fluid and the
dust particle clouds are suppose to be static at the
beginning. The dust particles are assumed to be spherical in shape and uniform in size and number density of the dust particle is taken as a constant throughout the flow.
The governing equations of unsteady two dimensional boundary layer incompressible flows of dusty fluids are given by

𝜕𝑢𝑓 𝜕 𝜕

phase. The momentum equation for particulate phase in normal direction, heat due to conduction and viscous
dissipation in the energy equation of the particle phase



+ 𝐹⃗ �𝑢 � + 𝐺⃗ �𝑢 � + 𝐻�𝑢 � = 𝑆�𝑢 , 𝑢 , 𝑇, 𝑇 � (2.1)

𝜕𝑡 𝜕𝑥 𝜕𝑦

𝜕𝑢𝑝 + 𝜕 𝐹⃗ �𝑢 � + 𝜕 𝐺⃗ �𝑢 � + 𝐻�𝑢 � = 𝑆 �𝑢 , 𝑢 , 𝑇, 𝑇 � (2.2)

𝜕𝑡

𝜕𝑥

𝑝 𝜕𝑦 𝑝

𝑝 𝑝

𝑓 𝑝 𝑝

have been considered for better understanding of the
boundary layer characteristics. The effects of volume fraction on skin friction, heat transfer and other boundary
Where 𝐻�𝑢𝑓 � = 0 , 𝐻�𝑢𝑝 � = 0
𝑢

2

𝜌𝑝 𝑢𝑝

layer characteristics also have been studied.The governing

𝐹⃗ �𝑢𝑓 � = �(1 − 𝜑)𝜌𝑢 �, 𝐹⃗ �𝑢𝑝 � = � 𝜌𝑝 𝑢𝑝 2 �

equation are reduced into system of ODEs and solved by
Shooting Techinique using Runge-Kutta Method with help
of FORTRAN-77.
𝜌𝑐𝑝 𝑢𝑇
𝑣

𝜌𝑝 𝑢𝑝 𝑣𝑝

𝜌𝑝 𝑐𝑠 𝑢𝑝 𝑇𝑝

𝜌𝑝 𝑣𝑝

𝐺⃗ �𝑢𝑓 � = �(1 − 𝜑)𝜌𝑢𝑣� , 𝐺⃗ �𝑢𝑝 � = � 𝜌𝑝 𝑢𝑝 𝑣𝑝 �

2.Mathematical Formulation and Solution: Consider an unsteady two dimensional laminar boundary layer flow of an incompressible viscous dusty fluid over a vertical stretching sheet .The flow is generated by the action of two equal and opposite forces along the x-axis and y-axis being normal to the flow . The sheet being stretched with the

𝜌𝑐𝑝 𝑣𝑇

𝜌𝑝 𝑣𝑝 2

𝜌𝑝 𝑐𝑠𝑣𝑝 𝑇𝑝

⎡ 𝜕
𝜕𝑢𝑝
0
𝜌𝑝 ⎤
⎢ 𝜕𝑦 �𝜑𝜇𝑠
⎢


𝜕𝑦 � + 𝜏𝑝 �𝑢 − 𝑢𝑝 � + 𝜑(𝜌𝑠 – 𝜌)𝑔 ⎥
⎥
𝑆𝑝 �𝑢𝑓 , 𝑢𝑝 , 𝑇, 𝑇𝑝 � = ⎢

𝜕
�𝜑𝜇
𝜕𝑣𝑝


𝜌
�𝑣 − 𝑣 �



⎢ 𝜕𝑦
⎢

𝑠 𝜕𝑦 � + 𝜏 𝑝 ⎥

2 2 ⎥

⎢ 𝜕 �𝜑𝑘
𝜕𝑇𝑝 𝜌𝑝 2
� − �𝑢 − 𝑢 � + 𝜑𝜇
�𝑢
𝜕 𝑢𝑝 + �𝜕𝑢𝑝 � � − 𝜌𝑝 𝑐𝑠 �𝑇
− 𝑇�⎥
⎣𝜕𝑦

𝑠 𝜕𝑦

𝜏𝑝 𝑝

𝑠 𝑝 𝜕𝑦2

𝜕𝑦
𝜏𝑇 𝑝 ⎦
⎡
⎢
𝑆�𝑢𝑓 , 𝑢𝑝 , 𝑇, 𝑇𝑝 � = ⎢


⎢

𝜕2 𝑢
𝜇 𝜕𝑦2 −

2

𝜌𝑝
𝜏𝑝
0
�𝑢 − 𝑢𝑝 � + 𝑔𝛽∗
⎤
(𝑇 − 𝑇∞ ) ⎥
⎥

2⎥

⎢𝑘 (1 − 𝜑) 𝜕 𝑇 + 𝜌𝑝 𝑐𝑠 �𝑇

𝜌𝑝
− 𝑇� + �𝑢

2 𝜕𝑢

− 𝑢� + 𝜇(1 − 𝜑) � � ⎥
⎣ 𝜕𝑦2
𝜏𝑇 𝑝
𝜏𝑝 𝑝
𝜕𝑦 ⎦

IJSER © 2015 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 184

ISSN 2229-5518

With boundary conditions


𝑐𝑥
𝑢 = 𝑈𝑤 (𝑥) = 1 − 𝑎𝑡 , 𝑣 = 0 𝑎𝑡 𝑦 = 0

𝜃 ′′ = 𝑃𝑟�2𝑓′ 𝜃 − 𝑓𝜃 ′ � − 2 𝛽
𝐻�𝜃𝑝 − 𝜃� −

𝑃𝑟𝐸𝑐 𝛽𝐻�𝐹 −

3 1−𝜑

2 2 𝐴

1−𝜑

& 𝜌𝑝 = 𝜔𝜌, 𝑢 = 0, 𝑢𝑝 = 0, 𝑣𝑝 → 𝑣 𝑎𝑠 𝑦 → ∞ (2.3)
𝑓′ �
− 𝑃𝑟𝐸𝑐 �𝑓′′ �
+ 𝑃𝑟 �𝜂𝜃′ (𝜂) + 4𝜃(𝜂)� (2.10)

2

Where 𝜔 is the density ratio in the main stream.

𝐴 ′ ′

⎡2 �𝜃𝑝 (𝜂)𝜂 + 4𝜃𝑝 (𝜂)� + 2𝐹 (𝜂)𝜃𝑝 + 𝐺(𝜂)𝜃𝑝 (𝜂)⎤
Similarly consider the non –dimensional temperature
boundary conditions as follows to solve 𝑇 𝑎𝑛𝑑 𝑇𝑝
𝜃 ′′ =
⎢

𝑃𝑟 ⎢

𝜖 ⎢

+𝛽 �𝜃𝑝 (𝜂) − 𝜃(𝜂)�

3 ′ 2

⎥
⎥
⎥ (2.11)

𝑐𝑥 2

⎢ + 𝐸𝑐 𝑃𝑟 𝛽 �𝑓
⎢ 3
(𝜂) − 𝐹 (𝜂)� ⎥

2 ⎥

𝑇 = 𝑇𝑤 = 𝑇∞ + 𝑇0 𝜈(1−𝑎𝑡)2 𝑎𝑡 𝑦 = 0

⎣ − 2
𝜖𝐸𝑐 𝑃𝑟 �𝐹(𝜂)𝐹′ ′(𝜂)+�𝐹′(𝜂)� � ⎦
𝑇 → 𝑇∞ , 𝑇𝑝 → 𝑇∞ 𝑎𝑠 𝑦 → ∞ (2.4)
With boundary conditions

′ (𝜂) = 0, 𝑓(𝜂) = 0 , 𝑓′ (𝜂) = 1 ,

For most of the gases 𝜏𝑝 ≈ 𝜏𝑇 , 𝐺
𝑘𝑠 = 𝑘

𝑐𝑠 𝜇𝑠

𝑐𝑝 𝜇

if 𝑐𝑠 =

𝑐𝑝

2

3𝑃𝑟

𝐹 (𝜂) = 0, 𝜃(𝜂) = 1, 𝜃𝑝 = 0 𝑎𝑠 𝜂 → 0 (2.12)
& 𝑓′ (𝜂) = 0, 𝐹(𝜂) = 0, 𝐺(𝜂) = −𝑓(𝜂)
Introducing the following non dimensional variables in
equation (2.1) to (2.2)
𝐻(𝜂) = 𝜔, 𝜃(𝜂) = 0, 𝜃𝑝 = 0𝑎𝑠 𝜂 → ∞

𝑢 = 𝑐𝑥

1−𝑎𝑡

𝑓′ (𝜂), 𝑣 = −� 𝑐𝜈

1−𝑎𝑡

𝑓(𝜂),

3. Solution Method:

𝑐𝑥



𝑢𝑝 = 1 − 𝑎𝑡 𝐹(𝜂), 𝑣𝑃 = �
𝑐𝜈
𝐺(𝜂),
Here in this problem the value of
𝑐
𝜂 = �𝜈(1 − 𝑎𝑡) 𝑦,
𝜑𝜌𝑠 =
𝜌

1 − 𝑎𝑡
𝜌 𝑝
= 𝜌𝑟 = 𝐻(𝜂),
𝜌
𝑓′′ (0), 𝐹(0), 𝐺(0), 𝐻(0), 𝜃 ′ (0), 𝜃𝑝 (0) are not known but
𝑓′ (∞) = 0, 𝐹(∞) = 0, 𝐺(∞) = −𝑓(∞), 𝐻(∞) = 𝜔, 𝜃(∞) = 0,
𝜃𝑝 (∞) = 0 are given. We use Shooting method to determine
the value of 𝑓′′ (0), 𝐹(0), 𝐺(0), 𝐻(0), 𝜃 ′ (0), 𝜃𝑝 (0) .We have
𝑃𝑟 =



𝜇𝑐𝑝 , 𝛽 =
𝑘

1 − 𝑎𝑡

𝑐𝜏𝑝

, 𝜖 = 𝜈𝑠 , 𝜑 =
𝜈

2

𝜌 𝑝
,
𝜌𝑠
supplied 𝑓′′ (0) =∝0 𝑎𝑛𝑑 𝑓′′ (0) =∝1 . The improved value
of 𝑓′′ (0) =∝2 is determined by utilizing linear interpolation
A = 𝑎 , 𝐸
= 𝑐𝜈
, 𝐹 = 𝑐 𝑥
, (2.5)
formula. Then the value of 𝑓′ (∝ , ∞) is determined by using

𝑐 𝑐

𝐶𝑝 𝑇0 𝑟

𝑔(1−𝑎𝑡)2

2

Runge-Kutta method. If 𝑓′ (∝2 , ∞) is equal to𝑓′ (∞ up to a

′′

𝑔𝛽∗ (𝑇𝑊 − 𝑇∞ )(1 − 𝑎𝑡)2
𝜌𝑠 𝜇
certain decimal accuracy, then ∝2 i.e 𝑓 (0) is determined,

𝐺𝑟 =
𝜃(𝜂) =
𝑇 − 𝑇∞


𝑐2 𝑥 , 𝛾 = 𝜌 , 𝜈 = 𝜌 ,
, 𝜃 (𝜂) = 𝑇𝑝 − 𝑇∞
otherwise the above procedure is repeated with ∝0 =
∝1 𝑎𝑛𝑑 ∝1 =∝2 until a correct ∝2 is obtained. The same
procedure described above is adopted to determine the

′

𝑇𝑤 − 𝑇∞
Where,
𝑐 𝑥2
𝑇𝑤 − 𝑇∞
𝑐𝑥2
correct values of 𝐹(0), 𝐺(0), 𝐻(0), 𝜃 (0), 𝜃𝑝 (0).
The solution of the present problem is obtained by


𝑇 − 𝑇∞ = 𝑇0 𝜈(1 − 𝑎𝑡)2 𝜃 , 𝑇𝑝 − 𝑇∞ = 𝑇0 𝜈(1 − 𝑎𝑡)2 𝜃𝑝
The equations (2.1) and (2.2) become

𝐻′ (𝜂) = − �𝐻(𝜂)𝐹(𝜂) + 𝐻(𝜂)𝐺′ (𝜂)� / �𝐴 𝜂 + 𝐺(𝜂)� (2.6)

2

2

numerical computation after finding the infinite value for η.
It has been observed from the numerical result that the
approximation to 𝜃 ′ (0) and 𝑓′′ (0)are improved by
increasing the infinite value of η which is finally
determined as η =10.0 with a step length of 0.125 beginning
from η = 0.Depends upon initial guess and number of steps
N. FORTRAN-77 is used to find the solutions of problem.
𝑓′′′ (𝜂) + 𝑓(𝜂)𝑓′′ (𝜂) − �𝑓′ (𝜂)�

− 𝐴 �𝑓′ (𝜂) + 𝜂 𝑓′′ (𝜂)� +

2

The value of 𝑓′′ (0) and 𝜃 ′ (0) are obtained from numerical

1

(1−𝜑)

𝛽 𝐻(𝜂) �𝐹 (𝜂) − 𝑓′ (𝜂)� + 𝐺𝑟 𝜃(𝜂) = 0 (2.7)
computation which is given in table – 1 for different
parameters used.

𝐴 �𝜂 𝐹′ (𝜂) + 𝐹(𝜂)� + �𝐹(𝜂)�2 + 𝐺(𝜂)𝐹′ (𝜂) − 𝜖𝐹′′ (𝜂) +

2

𝛽 �𝐹(𝜂)−𝑓′ (𝜂)� − 1 (1 − 1) = 0 (2.8)

𝐹𝑟 𝛾

𝐴 �𝜂𝐺′ (𝜂) + 𝐺(𝜂)� + 𝐺(𝜂)𝐺′ (𝜂) − 𝜖 𝐺 ′′(𝜂) + 𝛽 �𝑓(𝜂) +

2

𝐺(𝜂)� = 0 (2.9)

IJSER © 2015 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 185

ISSN 2229-5518

4. Graphical Representations:

Variation of Up w.r.t.β Ec=1.0,Pr=0.71,Fr=10.0,A=0.2, Gr=0.01,φ=0.01,γ=1200.0,є=3.0

0.2

0.15

Variation of θ w.r.t.Pr A=0.2,Ec=1.0,Fr=10.0,β=0.2, Gr=0.01,φ=0.01,γ=1200.0,є=3.0

1.5

1

0.1

0.05

0

β=0.01

β=0.02

β=0.03

0.5

0

-0.5

0 5 10

Pr=0.5

Pr=0.71

Pr=1.0

-0.05

0 5 10

Fig-1 η------------>

Fig-4 η----------------->

Variation of Up w.r.t.A Ec=1.0,Pr=0.71,Fr=10.0,β=0.2, Gr=0.01,φ=0.01,γ=1200.0,є=3.0

0.2

0.15

1.2

1

0.8

Variation of θ w.r.t.A β=0.01,Ec=1.0,Fr=10.0,φ=0.01, Pr=0.71,Gr=0.01,γ=1200.0,є=3.0

0.1

0.05

0

0 5 10

A=0.2

A=0.25

A=0.3

0.6

0.4

0.2

0

-0.2

0 5 10

A=0.2

A=0.25

A=0.3

-0.05

Fig-2 η---------------->

Fig-5 η--------------->

Variation of θ w.r.t.Ec A=0.2,Pr=0.71,Fr=10.0,β=0.2, Gr=0.01,φ=0.01,γ=1200.0,є=3.0

1.2

1

0.8

Variation of θp w.r.t.Ec β=0.01,A=0.2,Fr=10.0,φ=0.01, Pr=0.71,Gr=0.01,γ=1200.0,є=3.0

0.02

0.015

0.01

Ec=1.0

0.6

0.4

0.2

Ec=1.0

Ec=2.0

Ec=3.0

0.005

0

0 5 10

Ec=2.0

Ec=3.0

0

-0.2

0 2 4 6

Fig-3 η---------------------->

Fig-6 η--------------->

IJSER © 2015 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 186

ISSN 2229-5518

Variation of θp w.r.t.Pr β=0.01,A=0.2,Fr=10.0,φ=0.01, Ec=1.0,Gr=0.01,γ=1200.0,є=3.0

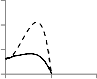
0.015

0.01

Variation of θp w.r.t.β Gr=0.01,A=0.2,Fr=10.0,φ=0.01, Ec=1.0,Pr=0.71,γ=1200.0,є=3.0

0.01

0.005

0

0 5 10

Pr=0.5

Pr=0.71

Pr=1.0

0.005

0

0 5 10

β=0.01

β=0.03

Fig-7 η------------------>

Fig-10 η--------------->

Variation of θp w.r.t.Gr β=0.01,A=0.2,Fr=10.0,φ=0.01, Ec=1.0,Pr=0.71,γ=1200.0,є=3.0

0.008

0.006

0.004

Gr=0.01

Variation of θp w.r.t.A β=0.01,Gr=0.01,Fr=10.0,φ=0.01, Ec=1.0,Pr=0.71,γ=1200.0,є=3.0

0.015

0.01

0.005

A=0.2

0.002

0

0 2 4 6

Fig-8 η-------------->

Gr=0.02

Gr=0.03

0

-0.005

0 2 4 6

Fig-11 η------------>

A=0.25

A=0.3

Variation of θp w.r.t.φ β=0.01,Gr=0.01,Fr=10.0,φ=0.01, Ec=1.0,A=0.2,Pr=0.71,γ=1200.0,є=3.0

0.008

0.006

0.004

0.002

0

0 2 4 6

φ=0.01

φ=0.02

Fig-9 η---------------->

IJSER © 2015 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 187

ISSN 2229-5518

TABLE-1 showing initial values of wall velocity gradient−𝑓′′ (0) 𝑎𝑛𝑑 𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒 𝑔𝑟𝑎𝑑𝑖𝑒𝑛𝑡 −𝜃′ (0)

5. Result and Discussion:

The set of non linear ODEs (2.6) to (2.11) with boundary condition (2.12) were solved using well known Runge- Kutta forth order algorithm with a systematic guessing of
𝑓′′ (0) and 𝜃 ′ (0) by the shooting technique until the
boundary condition at infinity are satisfied.The step size
0.125 is used while obtaining the numerical solution
accuracy up to the sixth decimal place i.e.1× 10−6, which is
very sufficient for convergence. In this method we choose
suitable finite values of 𝜂 → ∞ which depends on the
values of parameter used. The computations were done by
the computer language FORTRAN-77.The shear stress(
Skin friction coefficient)which is proportional to 𝑓′′ (0) and
rate of heat transfer(Nusselt number) which is proportional
to 𝜃 ′ (0) are tabulated in Table-1 for different values of
parameter used .It is observed from the table that shear
stress and rate of heat transfer decreases on the increase of
Ec , whereas it is increasing for increasing values of Pr.The Nusselt number decreases on the increasing of unsteady parameter ‘A’.The velocity profiles and temperature profiles also demonstrated graphically.
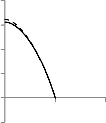
Fig-1 demonstrates the effect of β which infers that
increasing of β increases the particle phase velocity.Fig-2 shows that velocity profile of particle phase is decreasing on the increase of unsteady parameter A.
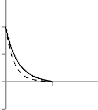
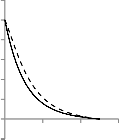
Fig-3 witnesses that increasing values of Ec, the temperature of fluid phase increases which shows effect on the boundary layer growth.
Fig-4 depicts the effect of Pr on temperature profile of fluid phase. From the figure we observe that, when Pr increase the temperature of fluid phase decreases which states that the viscous boundary layer thickness increases and thermal boundary layer thickness decreases.
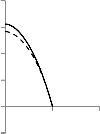
Fig-5 explains that the temperature of fluid phase decreases with increasing unsteady parameter ‘A’.
Fig-6 illustrates the effect of Ec on temperature profile of particle phase. It is evident that the increasing of Ec increases the temperature.
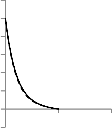
Fig-7 explains the effect of Pr on particle phase temperature, when Pr is increasing there is increasing of the temperature of particle phase.
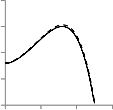
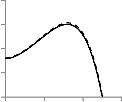
Fig-8 depicts the effect of Gr on particle phase temperature
profile which indicates that the increasing of Gr has
significant effect on particle phase temperature, enhancing
Gr, increases the temperature of particle phase.
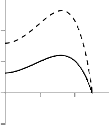
Fig-9 shows the effect of 𝜑 on temperature of particle phase.
It is evident that increasing in volume fraction increases the
temperature of particle phase which means thermal
boundary layer thickness increases.
Fig-10 illustrates the increasing β, increases the temperature
of dust phase.
Fig-11 describes that the temperature profile of particle phase increases on the increase of unsteady parameter A.6.

IJSER © 2015 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 188

ISSN 2229-5518

6. Conclusions:

The significant findings of the present study of the unsteady flow of a viscous, incompressible dusty fluid are presented below:
i. Increasing value of Ec is enhancing the temperature of both fluid phase as well as particle phase which indicates that the heat energy is generated in fluid due to frictional heating.
ii. The thermal boundary layer thickness of fluid phase
decreases on the increase of Pr. But the temperature of particle phase increases on increasing Pr. The temperature decreases at a faster rate for higher values of Pr which implies the rate of cooling is faster in case of higher prandtl number.
iii. The momentum boundary layer thickness decreases and thermal boundary layer thickness increases on the effect of Gr. If Gr =0 the present study will represent the horizontal stretching sheet.
iv. Increasing β increases the velocity and temperature
profiles of particle phase.
v. The increasing value of φ increases the temperature
profile of particle phase.
vi. The velocity of particle phase decreases on the
increase of unsteady parameter A.
vii. The temperature of fluid phase decreases and temperature particle phase increases on the increase of unsteady parameter A.
viii. We have investigated the problem using the values

7. References:

Greek Symbol

Subscripts

γ=1200.0, Fr=10.0, є=3.0.

Nomenclature:

[1] A.Aziz(2009), “ A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition” , Communications in Nonlinear Science and Numerical Simulation , vol.14,no.4,2009,pp.1064-1068
,doi:1016/j.cnsns.2008.05.003.
[2] B.J.Gireesha ,H.J.Lokesh ,G.K.Ramesh and C.S.Bagewadi(2011), “Boundary Layer flow and Heat Transfer of a Dusty fluid over a stretching vertical surface” , Applied Mathematics,2011,2,475-
481(http://www.SciRP.org/Journal/am) ,Scientific
Research.
[3] B.J.Gireesha, A.J. Chamakha, S.Manjunatha and
C.S.Bagewadi(2013), “ Mixed convective flow of a dusty fluid over a vertical stretching sheet with non uniform heat source/sink and radiation” ; International Journal of Numerical Methods for Heat and Fluid flow,vol.23.No.4,pp.598-612,2013
[4] B.J.Gireesha,G.S.Roopa and C.S.Bagewadi (2011), “Boundary Layer flow of an unsteady Dusty fluid and Heat Transfer over a stretching surface with non uniform heat source/sink ” , Applied Mathematics,2011

IJSER © 2015 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 189

ISSN 2229-5518

,3,726-735. (http://www.SciRP.org/Journal/am)
,Scientific Research.
[5] B.J.Gireesha,S.Manjunatha and C.S.Bagewadi(2014), “Effect of Radiation on Boundary Layer Flow and Heat Transfer over a stretching sheet in the presence of a free stream velocity”;Journal of Applied fluid Mechanics,Vol.7,No.1,pp.15-24,2014
[6] C.H.Chen(1998) , “Laminar Mixed convection Adjacent to vertical continuity stretching sheet, “Heat and Mass Transfer,vol.33,no.5-6,1998,pp.471-476.
[7] Chamakha,A.J.(2004).Unsteady MHD convective heat
and mass transfer past a semi-infinite vertical
permeable moving plate with heat absorption.Int.J.Engng.Sci.42,217-230.
[8] G.K.Ramesh , B.J.Gireesh and C.S.Bagewadi(2012), “Heat Transfer in M.H.D Dusty Boundary Layer flow of over an inclined stretching surface with non uniform heat source/sink ” ,Hindawi Publishing Corporation , Advances in Mathematical Physics,volume-2012,Article ID 657805,13 pages.
[9] Grubka L.J. and Bobba K.M(1985), “Heat Transfer
characteristics of a continuous stretching surface with
variable temperature” , Int.J.Heat and Mass Transfer , vol.107,pp.248-250 , 1985.
[10] H.I.Anderson,K.H.Bech and B.S.Dandapat(1992), “MHD flow of a power law fluid over a stretching sheet” , Int.J.of Nonlinear Mechanics,vol.27,no.6,pp.929-936,1992.
[11] H.Schlichting(1968), “Boundary Layer Theory” ,
McGraw-Hill , New York,1968.
[12] K.M.Chakrabarti(1974) , “Note on Boundary Layer in a
dusty gas” ,AIAA Journal , vol.12.no.8.pp.1136-
1137,1974.
[13] L.J.Crane(1970), “Flow past a stretching plate” ,
Zeitschrift fur Angewandte Mathematik und physic
ZAMP,VOL.2,NO.4,PP.645-647.1970.
[14] M.Das, B.K.Mahanta, R.Nandkeyolyar, B.K.Mandal
and K.Saurabh(2014), Unsteady Hydromagnetic flow of heat absorbing dusty fluid past a permeable vertical plate with ramped temperature. Vol.7, No.3, pp485-
492, 2014.
[15] N.Datta and S.K.Mishra(1982) , “Boundary layer flow of a dusty fluid over a semi-infinite flat plate” ,Acta Mechanica,vol.42.no1-2,1982,pp71-
83.doi:10.1oo7/BF01176514.
[16] Nandkeolyar, R.and M.Das(2013)Unsteady MHD flow
of a heat absorbing dusty fluid past a flat plate with ramped wall temperature. Afr. Mat. Article in Press.
[17] Saffman ,P.G.(1962), “On the Stability of Laminar flow
of a dusty gas” , Journal of Fluid Mechanics,13,120-128. [18] Sakiadis B.C (1961), “Boundary Layer behavior on continuous solid surface ; boundary layer equation for
two dimensional and axisymmetric flow” A.I.Ch.E.J,Vol.7,pp 26-28.
[19] Sharidan S. , Mahmood J. and Pop I. (2008), “Similarity solutions for the unsteady boundary layer flow and Heat Transfer due to a stretching sheet” , Int.J. of Appl.Mechanics and Engeenering,vol.11,No.3,pp 647-
654.
[20] Tsou,F.K,E.M. Sparrow , R.J. Glodstein (1967), “Flow and Heat Transfer in the boundary layer on a continous moving surface” , Int .J. Heat and Masstransfer,10,219-
235.
[21] Vajravelu , K. and Nayfeh(1992) , J. , “Hydromagnetic
flow of a dusty fluid over a stretching sheet” , Int.J. of nonlinear Mechanics,vol.27,No.6,pp.937-945.

Aswin Kumar Rauta was born in Khallingi of district

Ganjam, Odisha, India in 1981.He obtained the M.Sc. and M.Phil. degree in Mathematics from Berhampur university, Berhampur , Odisha, India. He has qualified NET in 2009 conducted by CSIR-UGC, government of India. He joined as a lecturer in Mathematics in the Department of Mathematics, S.K.C.G.College, Paralakhemundi ,Odisha,India in 2011 and is continuing his research work since 2009 and work till now. His field of interest covers the areas of application of boundary layer,heat/mass transefer and dusty fluid flows.Dr.Saroj Kumar Mishra was born in Narsinghpur of Cuttuck district,Odisha,India on 30th june 1952.He received his M.Sc. degree in Mathematics (1976) and Ph.D in Mathematics in 1982 on the research topic “Dynamics of two phase flow” from IIT Kharagpur, India . Currently he is working as Adjunct Professor of Mathematics at Centre for Fluid Dynamics Research, CUTM, Paralakhemundi, Odisha, India. He has authored and coauthored 50 research papers published in national and international journal of repute. He has completed one Major Research project and one Minor Research project sponsored by UGC, New Delhi, India. He has attended/presented the papers in national, international conferences. He is a member of several bodies like Indian Science Congress Association, Indian Mathematical Society, ISTAM, OMS, and BHUMS etc. His research interest includes the area of fluid dynamics, dynamics of dusty fluid particularly, in boundary layer flows, heat transfer, MHD, FHD and flow through porous media. His research interest also covers the nano fluid problems, existence and stability of problems and other related matters. Eight students have already awarded Ph.D degree under his guidance and another six students are working under his supervision.

IJSER © 2015 http://www.ijser.org