International Journal of Scientific & Engineering Research, Volume 2, Issue 2, February-2011 1
ISSN 2229-5518
A novel fast version of particle swarm optimization method applied to the problem of optimal capacitor placement in radial distribution systems
M.Pourmahmood Aghababa1, A.M.Shotorbani2, R.Alizadeh3, R.M.Shotorbani4
Abstract— Particle swarm optimization (PSO) is a popular and robust strategy for optimization problems. One main difficulty in applying PSO to real-world applications is that PSO usually needs a large number of fitness evaluations before a satisfying result can be obtained. This paper presents a modified version of PSO method that can converge to the optima with less function evaluation than standard PSO. The main idea is inserting two additional terms to the particles velocity expression. In any iteration, the value of the objective function is a criterion presenting the relative improvement of current movement with respect to the previous one. Therefore, the difference between the values of the objective function in subsequent iterations can be added to velocity of particles, interpreted as the particle acceleration. By this modification, the convergence becomes fast due to new adaptive step sizes. This new version of PSO is called Fast PSO (FPSO). To evaluate the efficiency of FPSO, a set of benchmark functions are employed, and an optimal capacitor selection and placement problem in radial distribution systems is evaluated in order to minimize cost of the equipment, installation and power loss under the additional constraints. The results show the efficiency and superiority of FPSO method rather than standard PSO and genetic algorithm.
Index Terms— convergence speed, fast PSO, capacitor placement, particle swarm optimization, radial distribution system
—————————— • ——————————
n recent years, many optimization algorithms are in- troduced. Some of these algorithms are traditional op-
timization algorithms. Traditional optimization algo- rithms use exact methods to find the best solution. The idea is that if a problem can be solved, then the algorithm should find the global best solution. Large search spaces increases the evaluation cost of these algorithms. There- fore the complex large spaces slow down the convergence rate of the algorithm to find the global optimum. Linear and nonlinear programming, brute force or exhaustive search and the divide and conquer methods are some of the exact optimization methods.
Other optimization algorithms are stochastic algo-
rithms, consisted of intelligent, heuristic and random me-
thods. Stochastic algorithms have several advantages
compared to other algorithms as follows [1]:
1. Stochastic algorithms are generally easy to imple-
ment.
————————————————
• Islamic Azad University Mamaghan Branch, Mamaghan, Iran, De- partment of Electrical Engineering; m.pour13@gmail.com
• Azerbaijan University of Tarbiat Moallem, Iran, Department of
Electrical Engineering; a.m.shotorbani@gmail.com
• Azerbaijan University of Tarbiat Moallem, Iran, Department of Elec- trical Engineering;ra_88ms@yahoo.com
• University of Tabriz, Iran, Department of Mechanical Engineering;
ramin.shotorbani@yahoo.com
2. They can be used efficiently in a multiprocessor environment.
3. They do not require the problem definition func-
tion to be continuous.
4. They generally find optimal or near-optimal solu-
tions.
Two well known intelligent stochastic algorithms are Particle swarm optimization (PSO) and genetic algorithm (GA). PSO is a population-based searching technique proposed in 1995 [2] as an alternative to GA [3]. Its devel- opment is based on the observations of social behavior of animals such as bird flocking, fish schooling, and swarm theory. Compared with GA, PSO has some attractive cha- racteristics. First of all, PSO has memory, that is, the knowledge of good solutions is retained by all particles, whereas in GA, previous knowledge of the problem is destroyed ones the population is changed. Secondly, PSO has constructive cooperation between particles, i.e. par- ticles in the swarm share their information.
In today’s power system, there is a trend to use nonli- near loads such as energy-efficient fluorescent lamps and
solid-state devices. Distribution systems provide power to a wide variety of load types. Resistive loads (power factor = 1.0) require no reactive power at all, while induc-
IJSER © 2010 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 2, Issue 2, February-2011 2
ISSN 2229-5518
tive loads (power factor < 1.0) require both active and reactive power. Inductive loads (e.g. motors) are always present so that the line current consists of a real (or resis- tive) component and an inductive component. Both com- ponents contribute to the MW losses (which are propor- tional to the square of the current magnitude), voltage drop and line loading (measured in A or MVA) reactive currents increased ratings for distribution components. The resistive component of the current cannot be substan- tially reduced as this is the part of the current that actual- ly performs work (defined by demand). The reactive component of the current can be reduced by installation of capacitors “close” to the loads. This has the effect that the reactive power needed is generated locally and the distribution circuits are relieved from the reactive power transfer. Effective placement of the shunt capacitors (de- pending on the situation) can improve the voltage profile and can greatly reduce the losses and the line loading. The capacitor sizing and allocation should be properly considered, or else they can amplify harmonic currents and voltages due to possible resonance at one or several harmonic frequencies. This condition could lead to poten- tially dangerous magnitudes of harmonic signals, addi- tional stress on equipment insulation, increased capacitor failure and interference with communication system. Thus, the problem of optimal capacitor placement con- sists of determining the locations, sizes, and number of capacitors to install in a distribution system such that the maximum benefits are achieved while operational con- straints at different loading levels are satisfied [4].
Optimal capacitor placement has been investigated since the 60’s. Early approaches were based on heuristic techniques applied to relaxed versions of the problem (some of the more difficult constraints were dropped). In the 80’s, more rigorous approaches were suggested as illustrated by the paper by Grainger [5], [6]. Baran-Wu [7] have formulated the capacitor placement problem as a mixed integer nonlinear program: the problem then has been approximated by a differentiable function that al- lowed the solution by Benders decomposition. In the 90’s, combinatorial algorithms were introduced as a means of solving the capacitor placement problem: simulated an- nealing has been proposed in [8], genetic algorithms in [9], and tabu search algorithms in [10]. Delfanti et. al. [11] have introduced a genetic algorithm (GA ) approach in VAR planning of a small CIGRE system of the Italian transmission and distribution network in order to deter- mine the minimum investment required to satisfy suita- ble reactive power constraints. Unfortunately the intro- duced GA algorithm had the problem of a large number of simplex iterations leading to very long computation time.
However, in this paper, a modified PSO, named fast
PSO (FPSO) is proposed which asserts fast convergence
property and consequently lower the number of function
evaluation. FPSO possesses two additional terms added
to the standard PSO velocity updating formula. These
statements cause FPSO to move to the optimal solution faster than the standard PSO, adaptively. Therefore, these modifications speed up the PSO convergence rate. The effectiveness and efficiency of the proposed FPSO is first examined using some well-known optimization bench- marks. Then, it is applied to the problem of optimal capa- citor placement in radial distribution systems. Numerical simulations are presented to validate the applicability and efficiency of our modified optimization scheme.
The rest of this paper is preceded as follows. Section 2 presents the standard PSO algorithm. Section 3 introduc- es FPSO. In Section 4, first the efficiency of FPSO algo- rithm is verified using some standard test functions. Then, the problem of optimal capacitor placement is solved using proposed FPSO method. Finally, some con- clusions are given in section 5.
A particle swarm optimizer is a population based stochas- tic optimization algorithm modeled based on the simula- tion of the social behavior of bird flocks. PSO is a popula- tion-based search process where individuals initialized with a population of random solutions, referred to as par- ticles, are grouped into a swarm. Each particle in the swarm represents a candidate solution to the optimiza- tion problem, and if the solution is made up of a set of variables, the particle can correspondingly be a vector of variables. In PSO system, each particle is “flown” through the multidimensional search space, adjusting its position in the search space according to its own experience and that of neighboring particles. The particle, therefore, makes use of the best position encountered by itself and that of its neighbors to position itself toward an optimal solution. The performance of each particle is evaluated using a predefined fitness function, which encapsulates the characteristics of the optimization problem [12].
The core operation of PSO is the updating formulae of
the particles, i.e. the equation of velocity updating and the
equation of position updating. The global optimizing
model proposed by Shi and Eberhart is as follows [12]:
vi+1=w×vi+RAND×c1×(Pbest-xi)+rand×c2×(Gbest-xi) (1)
xi+1=xi+vi+1 (2)
where w is the inertia weight factor, vi is the velocity of particle i, xi is the particle position and C1 and C2 are two positive constant parameters called acceleration coeffi- cients. RAND and rand are the random functions in the range [0, 1], Pbest is the best position of the ith particle and Gbest is the best position among all particles in the swarm.
The main drawback of PSO approach is slow convergence specifically prior to providing an accurate solution, close-
IJSER © 2010 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 2, Issue 2, February-2011 3
ISSN 2229-5518
ly related to its lack of any adaptive acceleration terms in the velocity updating formulae. In equation 1, c1 and c2 determine the step size of the particles movements through the Pbest and Gbest positions, respectively. In the original PSO, these step sizes are constant and for the all particles are the same.
In any iteration, the value of the objective function is a
criterion that presents the relative improvement of this
movement with respect to the previous one. Thus the dif-
ference between the values of the objective function in consequent iterations can represent the particle accelera- tion.
Therefore, velocity updating formulae turns to the fol- lowing form.
applied to all problems. Therefore, all parameters of FPSO should be determined optimally, by trial and er- ror.
3. There are three stopping criteria. The first one is related to the maximum number of allowable iterations set for the algorithm. The second one is when no improvement has been made for a certain number of iterations in the best solution, and the third one is when a satisfactory solution is found.
4. The fast version of PSO is proposed for continuous va-
riable functions. Moreover, the main idea of speeding up can be applied to the discrete form of the PSO [13]. We take this into our consideration as a future work.
5. Increasing the value of the inertia weight, w, would in-
crease the speed of the particles resulting in more explo- ration (global search) and less exploitation (local
vi+1 = w×vi + (f(Pbest) - f(xi )) × RAND× c1 × (Pbest -
xi) + (f(Gbest) - f(xi)) × rand × c2 × (Gbest - xi)
(3)
search). On the other hand, decreasing the value of w
will decrease the speed of the particle resulting in more
where f(Pbest) is the best fitness function that is found by ith
particle and f(Gbest) is the best fitness function that is
found by swarm up to now and other parameters are chosen the same as section A. These two terms, i.e.
(f(Pbest) - f(xi )) and (f(Gbest) - f(xi)) cause to have an adaptive
movement. w
exploitation and less exploration. Thus, an iteration- dependent weight factor often outperforms a fixed fac- tor. The most common functional form for this weight factor is linear, and changes with step i as follows:
wmax - wmin
= wmax -
The steps of FPSO algorithm are as follows:
1. Initialize particles positions and velocities, ran-
i+1
![]()
N iter
(4 )
domly.
2. Calculate the objective functions values of par-
ticles.
3. Update the global and local best positions and
their objective function values.
4. Calculate new velocities using equation (3).
5. Update the positions.
6. If stop condition is attained stop otherwise go to
step 2.
1. The term (f(Pbest) - f(xi)) and (f(Gbest) - f(xi)) are named local and global adaptive coefficients, respectively. In any iteration, the former term defines the movement step size in the best position’s direction which is found by ith particle, and the later term defines adaptive movement step size in the best optimum’s direction point which ever have been found by the swarm. In oth- er words, the adaptive coefficients decrease or increase the movement step size relative to being close or far from the optimum point, respectively. By means of this method, velocity can be updated adaptively instead of being fixed or changed linearly. Therefore, using the adaptive coefficients, the convergence rate of the algo- rithm will be increased rather than performed by the proportional large or short steps.
2. Stochastic optimization approaches suffer from the problem of dependent performance. This dependency is usually because of parameter initializing. Thus, we ex- pect large variances in performance with regard to dif- ferent parameter settings for FPSO algorithm. In gen- eral, no single parameter setting exists which can be
where Niter is the maximum number of iterations and Wmax
and Wmin are selected to be 0.8 and 0.2, respectively.
6. Lastly, the proposed FPSO is still a general optimiza-
tion algorithm that can be applied to any real world continuous optimization problems. In the next section, we will apply FPSO approach to several benchmark functions and compare the results with standard PSO and GA algorithms.
In this section, first the efficiency of FPSO is tested using a set of test functions. Then, the FPSO algorithm is ap- plied to solve the problem of optimal capacitor place- ment.
Here, some well-known benchmark functions (listed in Appendix A) are used to examine the effectiveness and convergence speed of the proposed FPSO technique. To avoid any misinterpretation of the optimization results, related to the choice of any particular initial popula- tions, we performed each test 100 times, starting from various randomly selected solutions, inside the hyper rectangular search domain specified in the usual litera- ture.
The performance of FPSO is compared to continuous
GA and PSO algorithms using 15 functions listed in Ap- pendix A. The experimental results obtained for the test functions, using the 3 mentioned different methods, are given in Table 1. In our simulations, each population in GA has 10 chromosomes and a swarm in FPSO and PSO
IJSER © 2010 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 2, Issue 2, February-2011 4
ISSN 2229-5518
70
has 10 particles. Other parameters of the three algo-
rithms are selected optimally by trial and error. For each 60
function, we give the average number of function evalu-
ations for 100 runs. The best solution found by 3 me- 50
thods was similar, so there are not given here.
Note that the FPSO has shown drastically better re- 40
sults in convergence and evaluation costs compared
30
with GA and PSO, as it utilizes adaptive movements to
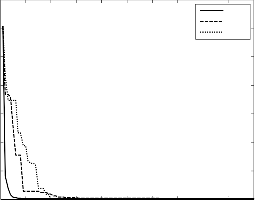
reach to the optima, while GA and PSO do not have 20 such an element. Fig. 1 shows a typical diagram of three algorithms convergence rates for B2 function, starting 10 from a same initialization point. As it can be seen, al-
FPSO
PSO GA
though, all algorithms can find the optima, but FPSO is dramatically faster than the others. Therefore, in many real world applications where real time computations and less CPU time consumption are necessary, FPSO may work better than GA and PSO.
TABLE 1
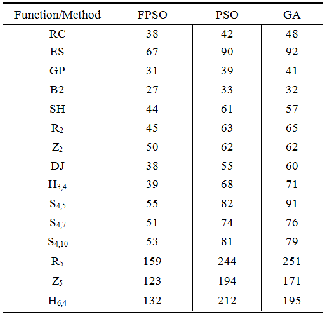
AVERAGE NUMBER OF OBJECTIVE FUNCTION EVALUATIONS USED BY THREE METHODS
0
0 10 20 30 40 50 60 70 80 90 100
iteratrion number
Fig. 1. Convergence rate of three algorithms for B2 function
Now that the efficiency and high speed convergence property of the proposed FPSO algorithm has been re- vealed by simulation results of benchmark functions, the next step is to solve the problem of optimal capacitor placement with FPSO method.
The optimal capacitor placement problem has many
variables including the capacitor size, capacitor location and capacitor equipment and installation costs. In this section we consider a distribution system with nine possible locations for capacitors and 27 different sizes of capacitors. Capacitor values are often assumed as conti- nuous variables whose costs are considered as propor- tional to capacitor size in past researches [14-16]. How- ever, commercially available capacitors are discrete ca- pacities and tuned in discrete steps. Moreover, the cost of capacitor is not linearly proportional to the size. Hence, if the continuous variable approach is used to choose integral capacitor size, the method may not re- sult in an optimum solution and may even lead to unde- sirable harmonic resonance conditions [17]. However, considering all variables in a nonlinear fashion will make the placement problem very complicated. In order to simplify the analysis, only fixed-type capacitors are considered with the following assumptions: (1) balanced conditions; (2) negligible line capacitance; and (3) time- invariant loads. The objective function of this problem is to minimize f. It is composed of two parts: (1) the cost of the power loss in the transmission branch and (2) the cost of reactive power supply. Therefore, the fitness function is defined as [18].
m
f = K p ploss + n =1Qcj n K cj n
(5 )
where Kp is the equivalent annual cost per unit of power
loss ($/KWatt), n is the bus number,
Kcjn is the equiva-
IJSER © 2010 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 2, Issue 2, February-2011 5
ISSN 2229-5518
lent capacitor cost installed in bus n ($/KVar),
Start
Qcjn = j
K s is the size of the capacitor, Ks is the capa-
citor bank size (KVar) (here Ks=150), and j= the number of banks used in any bus.
Here, a radial distribution feeder is used as an exam- ple to show the effectiveness of this algorithm. The test- ing distribution system is shown in Fig. 2.
This feeder has nine load buses with rated voltage of
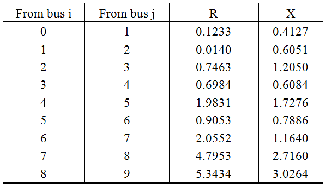
23 kV. Tables 2 and 3 show the loads and feeder line
constants. Kp is selected to be US$ 168/kW. The base
value of voltage and power is 23 kV and 100 MW re-
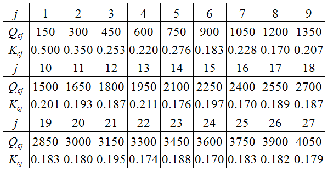
spectively [18]. Possible choice of capacitor sizes and costs are shown in Table 4 by assuming a life expectancy of 10 years (the placement, maintenance, and running costs are assumed to be grouped as total cost). The main procedure of finding optimal capacitor placements with FPSO method is illustrated in Fig. 3.
Select parameters of FPSO
Generate the randomly positions and velocities of particles
Initialize, pbest with a copy of the position for particle, determine gbest
Update velocities and positions according to Eqs (2), (3)
Evaluate the fitness of each particle
update pbest and gbest
Supply source
1 2 3 4 5 6 7 8 9
Satisfying stopping criterion
Optimal capacitor placements
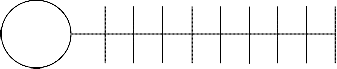
Fig. 2. Testing distribution system with nine buses
End
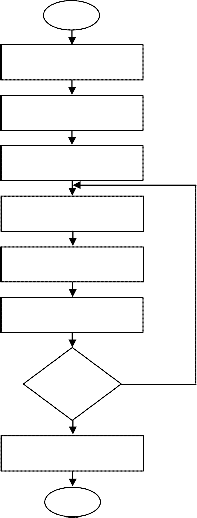
Fig. 3. Flow chart of optimal capacitor placements with FPSO
IJSER © 2010 http://www.ijser.org
TABLE 2
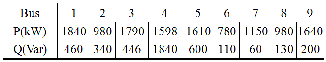
LOAD DATA OF THE TEST SYSTEM
TABLE 3
FEEDER DATA OF THE TEST SYSTEM
International Journal of Scientific & Engineering Research, Volume 2, Issue 2, February-2011 6
ISSN 2229-5518
TABLE 4
POSSIBLE CHOICE OF CAPACITOR SIZES AND COSTS
The effectiveness of the method is illustrated by a comparative study of the following two cases: Case 1 is without capacitor installation and Case 2 use the FPSO approach for optimizing the size and the placement of the capacitor in the radial distribution system.
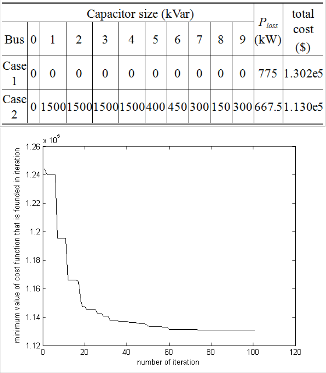
The capacitor sizes, power loss and the total cost are
shown in Table 5. Fig. 4 depicts the minimum value of
cost function in any iteration for 100 iterations. Before
In this paper, a modified optimization technique based on PSO algorithm is introduced and it is called fast PSO (FPSO). Using adaptive coefficients, the step sizes of particles movements are changed appropriately to reach the optima, rapidly. The important characteristics of FPSO are: less function evaluation and high convergence rate. Consequently in real time processes, FPSO seems to outperform both the standard PSO and the genetic algo- rithm. The efficiency of the proposed FPSO algorithm is shown using several well-known benchmark functions. Then, the proposed FPSO method is used to successfully solve the problem of optimal capacitor selection and placement problem in radial distribution systems.
Some well-known benchmark functions of optimiza- tion problems [19].
Branin RCOS (RC) (2 variables):
optimization (Case 1), the power loss is 775 kW and total
5![]()
= -
2
+ =5
cost is 1.302e5 $. After optimization (Case 2), the power
RC( x , x )
x x 2
x1 - 6 +
loss becomes 667.5 kW and the total cost becomes
1 2 2
4n 2 1
n
1.130e5 $.
10 1 - 1
cos( x
) + 10;
![]()
8n 1
TABLE 5
SUMMARY RESULT OF THE APPROACH
Search domain: -5 < x1 <10, 0 < x2 < 15
no local minimum; 3 global minima
B2 (2 variables):
B2( x , x
) = x 2 + 2x 2 - 0.3 cos( 3nx1 ) - 0.4 cos( 4nx2 ) + 0.7;
1 2 1 2
Search domain: -100 < xj < 100, j=1, 2; several local minima; 1 global minimum Easom (ES) (2 variables):
ES( x1 , x2 ) = - cos( x1 ) cos( x2 ) exp( -(( x1 - n )2 + ( x2 - n )2 ));
Search domain: -100<xj<100, j=1, 2;
several local minima, 1 global minimum
Goldstein and Price (GP) (2 variables):
GP( x1 , x2 ) =
T1 + ( + x1 + x2 + 1 )2
( 19 - 14 x
+ 3x 2 - 14 x
+ 6 x x
+ 3 x 2 )
L 1 1
2 1 2 2 J
T30 + ( 2 x1 - 3x2 ) 2
;
( 18 - 32 x
+ 12x 2 + 48 x
- 36 x x
+ 27 x\2 )
L 1 1
2 1 2 2 J
Search domain: -2 < xj < 2, j=1, 2;
4 local minima; 1 global minimum
Shubert (SH) (2 variables):
SH ( x1
, x2
) =
5
j =1
j cos[( j + 1 )x1
+ j ]
Fig. 4. Minimum value of cost function in each iteration
5
j =1
j cos[( j + 1 )x2
+ j ] ;
Search domain: -10 < xj < 10, j=1, 2;
760 local minima; 18 global minimum
IJSER © 2010 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 2, Issue 2, February-2011 7
ISSN 2229-5518
De Joung (DJ) (3 variables):
DJ ( x1 , x 2 , x3 ) = x 2 + x 2 + x 2
1 2 3
Search domain: -5.12 < xj < 5.12, j=1, 2, 3;
1 single minimum (local and global)
Hartmann (H3, 4) (3 variables):
capacitor placement using deterministic and genetic algorithms,” Pow- er Industry Computer Applications, 1999. PICA '99. Proc. of the 21st IEEE International Conference, pp. 331-336, 1999
[12] Y. Shi and R. Eberhart, “A modified particle swarm optimizer,” Proceed-
ings of the IEEE international conference on evolutionary computation, Pisca- taway, NJ: IEEE Press, pp. 69–73, 1998.
[13] J. Kennedy and R. Eberhart, “A Discrete Binary Version of the Particle
H 3 ,4 ( x1 , x2 , x3 ) = -
4
j =1
ci exp[ -
3
j =1
aij ( xi - pij ) 2 ] ;
Swarm Algorithm,” In Proceedings of the Conference on Systems, Man, and
Cybernetics, pp. 4104-4109, 1997.
Search domain: 0 < xj < 1, j=1, 2, 3;
4 local minima1 global minimum
Shekel (S4, n) (3 variables):
[14] Y. Baghzouz and S. Ertem, “Shunt capacitor sizing for radial distribu- tion feeders with distorted substation voltages,” IEEE Trans Power Deli- very, vol. 5, no. 2, pp. 650–656, 1990.
[15] J. J. Grainer and W. D. Stevenson, Power system analysis, New York:
S 4 ,n ( X ) = -
n
j =1
[( X - ai )T
( X - ai ) + ci ] -1 ;
McGraw-Hill, ISBN No. 0-07-113338-0, 1991.
[16] Y. Baghzouz, “Effects of nonlinear loads on optimal capacitor place-
X = ( x , x
, x , x
)T ; a
= ( a1 , a 2 , a 3 , a 4 )T ;
ment in radial feeders,” IEEE Trans Power Delivery, vol. 6, no. 1, pp. 245–
1 2 3 4
i i i i i
251, 1991.
Search domain: 0 < xj < 10, j=1, 2, 3,4;
n local minima; 1 global minimum
Rosenbrock (Rn) (n variables):
[17] S. Sundhararajan and A. Pahwa, “Optimal selection of capacitors for radial distribution systems using a genetic algorithm,” IEEE Trans Pow- er Systems, vol. 93, pp. 1499–1507, Aug 1994.
[18] T. S. Chung and H. C. Leung, “Agenetic algorithm approach in optimal
R ( X ) = - n
- [ 100( x 2 - x j 1 )2 + ( x j - 1 )2 ;
capacitor selection with harmonic distortion consideration,” Elsevier,
n j =1 j +
Search domain: -5 < xj < 10, j=1, …, n;
several local minima;1 global minimum
Zakharov (Zn) (n variables):
Electrical Power and Energy systems, vol. 21, pp. 561-569, 1999.
[19] R. Chelouah and P. Siarry, “Genetic and Nelder-Mead Algorithms hybridized for a More Accurate Global Optimization of Continuous Multiminima Functions,” European Journal of Operational Research, vol.
148, pp. 335-348, 2003.
Z n ( X ) =
n
j =1
x 2 + (
n
j =1
0.5 jx j
)2 + (
n
j =1
0.5 x j
)4 ;
Search domain: -5 < xj < 10, j=1, …, n;
several local minima; 1 global minimum.
[1] M. Lovberg and T.Krink, “Extending Particle Swarm Optimizers with Self-Organized Criticality,” In Proceeding of Forth Congress on Evolutio- nary Computation, vol. 2, pp.1588- 1593, 2002.
[2] J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” In Proceed-
ings of IEEE International Conference on Neural Networks, Perth, Australia, vol.4, pp.1942-1948, 1995.
[3] J.H. Holland, Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor, MI, Internal Report, 1975.
[4] H. N. Ng, M. M. A. Salama, A. Y. Chikhani, “Capacitor Allocation by
Approximate Reasoning: Fuzzy Capacitor Placement,” IEEE Transac- tions on Power Delivery, vol. 15, no. 1, pp. 393 - 398, Jan 2000.
[5] J. J. Grainger and S. H. Lee, “Capacity release by shunt capacitor place- ment on distribution feeders: A new voltage-dependent model,” IEEE Trans. Power Apparatus and Systems, vol. PAS-101, no. 15, pp. 1236–1244, May 1982.
[6] J. L. Bala, P. A. Kuntz, and M. J. Pebles, “Optimal capacitor allocation
using a distribution-recorder,” IEEE Trans. Power Delivery, vol. 12, no. 1, pp. 464–469, Jan 1997.
[7] M. Kaplan, “Optimization of number, location, size, control type, and control setting of shunt capacitors on radial distribution feeders,” IEEE Trans. Power Apparatus and Systems, vol. PAS-103, no. 9, pp. 2659–2663, Sept 1984.
[8] H. D. Chiang, J. C. Wang, O. Cockings, and H. D. Shin, “Optimal capa-
citor placement in distribution systems—Part I: A new formulation and the overall problem,” IEEE Trans. Power Delivery, vol. 5, no. 2, pp. 634–
642, Apr 1990.
[9] S. Sundhararajan and A. Pahwa, “Optimal selection of capacitors for
radial distribution systems using a genetic algorithm,” IEEE Trans. Pow-
er Systems, vol. 9, no. 3, pp. 1499–1505, Aug 1994.
[10] Y. C. Huang, H. T. Yang, and C. L. Huang, “Solving the capacitor
placement problem in a radial distribution system using tabu search approach,” IEEE Trans. Power Syst., vol. 11, no. 4, pp. 1868–1873, Nov
1996.
[11] M. Delfanti, G. P. Granelli, P. Marannino and M. Montagna, “Optimal
IJSER © 2010 http://www.ijser.org