International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1405

ISSN 2229-5518

AVAILABILITY ANALYSIS OF A TWO-UNIT STANDBY SYSTEM WITH DELAYED REPLACEMENT UNDER PERFECT SWITCHING

VIRESH SHARMA DIGVIJAY SINGH Department of Mathematics Department of Mathematics

J.P.Institute of engineering & tech.,Meerut N.A.S.(P.G.) College, Meerut drdigvijay2008@rediffmail.com vireshsharma1@yahoo.com

ABSTRACT: In this paper, the author has initiated the study of availability of the system which consists of two identical cold standby units with constant failure rates. Initially, one unit is operative while other remains as standby. Each of the units of the system has three modes, i.e., normal, degraded and total failure. The system fails when both the units fail totally and may also fail due to common cause failure. The time taken in replacement of a failed unit by a standby unit is not negligible but is a random variable.
KEYWORDS: Standby system, Repairable system,
(v) Failure time distributions are negative exponential, while the repair and delay time distributions are arbitrary.
(vi) A single service facility is available to repair a D-unit, a F-unit and to activate the cold standby unit. The repair facility is not always with the system but can be made available instantaneously whenever needed.
(vii) Initially system works with normal efficiency
Supplimentry variable.

IJSEaRfter inspection.

INTRODUCTION : The author has considered here, a
complex system having two identical cold standby units with constant failure rates. Initially, one unit is operative while other remains as standby. Each of the units of the system has three modes. i.e., normal, degraded and total failure. The
system fails when both the units fail totally and may also fail
(viii) A repaired unit works as good as new.

NOTATIONS:

due to common cause failure. The time taken in replacement of a failed unit by a standby unit is not negligible but is a random variable. Failure time distribution of the units are exponential while inspection rates, replacement rate and repair rate time distributions are quite general. Reliability parameters, generally mean time to systems failure (MTSF) and availability in such systems have also been obtained using the theory of Semi-Markov process and supplementary variable process. The purpose of the present chapter is to discuss a two-unit cold standby with three modes dissolving the above two very stringent assumptions.

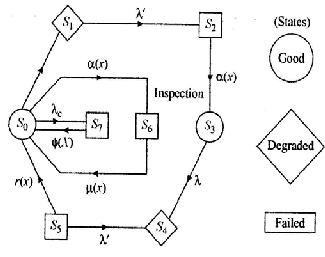
SYSTEM DESCRIPTION :

(i) A cold standby system comprises two similar units. Each unit has three modes: normal (N), Degraded (D) and total failure (F). The units are said to be N,D and F units if they are in their respective modes.
(ii) The replacement time of a failed unit is not negligible but is a random variable called delay time.
(iii) The system fails on the total failure of its both units and also breaks down completely due to

D / Dt / Dx

λ / λ '

λc

α ( x ) / µ ( x )

r ( x ) / φ ( x )

β ( x ) ( )

d / ∂ / ∂

: dt ∂t ∂x

: Constant failure rates from N
to D/D to F
:Constant common cause failure rate

: Inspection rate from 0 to

S6 / S6 to S0

: General repair rate from 5

S / S S

to 0 7 to 0

: Switching rate from 2 to

common cause failure.
(iv) In the normal state, the system is inspected with the general inspection rate distribution.

P t

i : Probabilities in the i

where i= 1, 3, 4
state

International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1406

ISSN 2229-5518

P2 ( x, t )

TRANSITION DIAGRAM:

: Probabilities at the i
where i = 0, 2, 5, 6, 7.
state

 Dx + Dt + µ ( r ) P6 ( x, t ) = 0

(7)

 Dx + Dt + φ ( x ) P7 ( x, t ) = 0

(8)
These equations are to be solved under following boundary and initial conditions:

Boundary Conditions :

∞ ∞ ∞

P0 (0, t ) = ∫

P5 ( x, t ) r (t ) dx + ∫

P7 ( x, t )φ ( x) dx + ∫

P6 ( x, t ) µ ( x) dx

0 0 0

(9)

P2 (0, t ) = λ ' P1 (t )

(10)

FORMULATION OF MATHEMATICAL PROBLEM : Viewing the

P5 (0, t ) = λ ' P4 (t )

(11)

IJSER

nature of this system, we obtain the following set of
difference differential equations by connecting the state

P6 (0, t ) = ∫

P0 ( x, t )α ( x ) dx

probabilities at time t + ∆ with those at time t and taking limits as ∆t → 0 .

 Dx + Dt + λ + λc + α ( x ) P0 ( x, t ) = 0

7 ( )

c 0 ( )

(12)

P 0, t

= λ P t

(13)
(1)

Initial Conditions :

[ D + λ '] P1 (t ) = λ P0 (t )

(2)

P0 (0) = 1

Pk ( 0 ) = 0

∀ ( k ≠ 0)

 Dx + Dt + β ( x ) P2 ( x, t ) = 0

(3)

SOLUTION OF THE PROBLEM : Taking Laplace transform of equations (1) through (13) and solving one by one, using initial conditions and after minor simplification, one may obtain

[D + λ ] P3 (t ) = ∫

β P2 ( x, t ) dx

[D + λ ] P4 ( s ) = λ P3 (t )

(4)
(5)

P0 ( s ) =

B ( s )

A ( s )

(14)

 Dx + Dt + r ( x ) P5 ( x, t ) = 0

(6)

P1 ( s ) =

s + λ '

B ( s )

A ( s )

(15)

International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1407

ISSN 2229-5518

P ( s ) =

λλ ' . B ( s ) .D

( s )

P ( s ) = P ( s ) + P ( s ) + P ( s ) + P ( s ) = 1 − P

( s )

2 s + λ '

A ( s ) β

(16)

down

2 5 6 7

s up

(23)

λλ '

B ( s ) β

It is worth noticing that

P3 ( s ) = ( s + λ ) ( s + λ ') . A ( s ) .S

( s )

P ( s ) + P

( s ) = 1

(17)

up down

(24)

P ( s ) =

λ 2λ '

B ( s ) β

. .S

( s )

ERODIC BEHAVIOUR OF THE SYSTEM : Using Abel’s Lemma

viz., lim SF ( S ) = lim F (t ) = F ( say )

4 ( s + λ ) ( s + λ )2

A ( s )

s →0

t →∞

; provided

( ) 2 '2

B ( s )

(18)

( ) ( )

limit on R.H.S. exists, the following time independent
probabilities have been obtained from equations (14)
through (22).

B ( 0 )

P5 s

= λ λ

( s + λ ')2 ( s + λ )

. .S β

A ( s )

s .Dr s

(19)

P0 =

A ' ( 0 )

(25)

S (s + λ + λc )

λ B ( 0 )

P6 ( s ) =

A ( s )

.Dµ ( s )

P1 = λ ' . A ' ( 0 )

7 λ IA ( s ) Jφ

(20)

Rλ ' (0)

(26)

P ( s ) = λc . B ( s ) .D

( s )

B (0)

P = λ. M β

Where

A(s) = 1

λ2λ '2

(s + λ )(s + λ ')2

(21)

.S β (s) − S r (s) − S α (s + λ + λ ).S µ (s) − λ B (s)S φ (s)

P3 =

B ( 0 )

A ' ( 0 )

(27)
(28)

B ( s ) = Dα ( s + λ + λc )

P4 =

λ B ( 0 )

λ ' A ' ( 0 )

(29)

Dθ ( s )

1 − S

( s )

P = λ.

B (0) r

EVALUATION OF LAPLACE TRANSFORMS OF PROBABILITIES

UP AND DOWN STATES :

PUP ( s ) = P0 ( s ) + P1 ( s ) + P3 ( s ) + P4 ( s )

5 A ' (0)

P = S (λ + λc ) M µ

(30)

B (s ) 

λ λλ ' ( )

λ 2λ ' ( )

6 A ' (0)

(31)

= 1− + S β

s + .S β s 

A(s ) 

s + λ '

(s + λ )(s + λ ')

(s + λ )(s + λ ') 

(22)

International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1408

ISSN 2229-5518

P = =λc .

B (0) φ

λ 2λ '2

D ( s ) β 2

7 λ A ' (0)

(32)

P ( s ) =

( s + λ ) ( s + λ ')

. . .

C ( s ) ( s + β )

s + r

5 2

P = A

2B (0) 

= 1 +

λt 



(39)

up vss

A ' (0)  λ 

(33)

P6 ( s ) =

( s + α + λ + λc )

. 1

C ( s )

. 1

s + µ

Where

B (0) =  β ( s )

s =0

P7 ( s ) =

λ D ( s )

c . .

(40)

A ' (0) =  d

 ds

A ( s )

 s =0

λ C ( s )

s + φ

(41)
And

Avss = Availability at t = ∞

M ' (i = β , r, µ,φ ) = S α (0)

Where

C (s) = 1−

λ2λ '2 D (s) β

. r − αµ

− λ D (s) φ

PARTICULAR CASES : (When repair follows exponential time distribution)

(s + λ )(s + λ ')2 (s + β ) (s + r)

(s + α + λ + λc )(s + µ )

(s + φ )

setting

S x ( s ) =

s + x

D ( s ) = 1

s + α + λ + λ

IJSERc

Where we get

x = β , r,φ ,α , µ

in equations (14) through (21),

RELIABILITY AND MTTF :

P ( s ) = D ( s )

R ( s ) =

1 1 + λ

 

0 C ( s )

D ( s )

(34)

(s + α + λ + λc ) 

s + λ ' 

(42)

P1 ( s ) = ( s + λ ) . C ( s )

MTTF = lim R ( s ) =

1  

1 +

(35)

s →0

(α + λ + λc ) 

λ ' 

(43)

λλ '

D ( s )

For a complex configuration having parametric values

P2 ( s ) = ( s + λ ) ( s + β ) . C ( s )

(36)

λ = 0.01 ,

λ ' = 0.02 ,

α = 0.8

λλ '

D ( s ) β

P3 ( s ) = ( s + λ ) ( s + λ ') . C ( s ) . ( s + β )

(37)

P ( s ) =

λ 2λ '

D ( s ) β

. .

4 ( s + λ ) ( s + λ ')2

C ( s ) ( s + β )

(38)

International Journal of Scientific & Engineering Research, Volume 4, Issue 12, December-2013 1409

ISSN 2229-5518

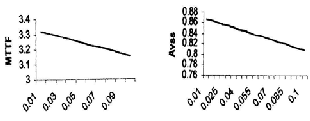
Fig.1. MTTF vs Failure Fig. 2. Avss vs Failure

REFERENCES :

1. Dummer, G. and N. Griffin, Electronic Equipment
Reliability, John Wiley and Sons, N.Y. (1960)
2. Fukula, I. And M. Kodama, Mission reliability for a redundant repairable system with two dissimilar units. IIE Trans on Reliability. R-23(1974).
3. Bazoksky, I., Reliability Theory of Prentice Hall Inc., Englewood eliffs, New Nersey (1961)

IJSER