International Journal of Scientific & Engineering Research, Volume 3, Issue 3, March-2012 1
ISSN 2229-5518
A simple method for calculation of the bulk modulus of boron-doped diamond
Dr. V. Katsika-Tsigourakou
Abstract— Boron-doped diamond undergoes an insulator-metal transition at some critical value (around 2.21 at %) of the dopand concentration. Here, we report a simple method for the calculation of its bulk modulus, based on the thermodynamical model, by Varotsos and Alexopoulos, that has been originally suggested for the interconnection between the defect formation parameters in solids and bulk properties. The results obtained at the doping level of 2.6 at %, which was later improved at the level 0.5 at %, are in agreement wi th the experimental values.
Index Terms— Compressibility, Point defects, Mixed crystals, Elastic properties, Defect volume, Activat ion energy, Boron-doped diamond
1 INTRODUCTION
—————————— ——————————
IN a very recent careful work, Pandey, Alam and Kumar
[1] studied the pseudo elastic behavior of liquid alloys us-
ing pseudo potential model based on the density functional theory with both the local density approximation and the generalized gradient approximation for the exchange corre- lation function. Very interesting results were obtained which showed that the elastic constants of the elemental cubic model depend primarily on the bonding variance, the density at the cell boundary and the symmetry of the lat- tice.
In the above paper Pandey et al. applied the model
of Varotsos and Alexopoulos using slight modification in volume due to concentration. It is the scope of this short paper to extend the usefulness of the challenging findings of Pandey et al. and show that the use of Varotsos and Alexopoulos model can also serve for treating a problem (see below) of major technological interest.
Diamond has been extensively studied (e.g., see
[2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12]) in view of its
remarkable properties. For example, it has a very large De-
bye temperature [13] and the largest elastic moduli known
for any material and correspondingly the largest sound velocities [13], [14]. Nowdays, the diamond anvil cell (DAC) technique, which is extensively used as a unique tool for producing high pressure in the laboratory [15], ex- ploits the extreme hardness of diamond.
Diamond is a wide band-gap semiconductor. The high interest of studying both doped natural diamonds and high-level doped synthetic diamonds [16] originates from the discovery of the profound influence of dopants on their physical properties. Specifically, doping diamond with bo- ron leads to the insulator-metal transition [17]. Electrical conductivity measurements of diamond revealed that for boron concentrations higher than some critical value esti- mated as 2.21 at %, the conductivity on the metallic side of the transition at low temperature a Tb law. For metallic samples, b was found to be 1/3, approaching 1/2 at higher concentrations [17]. Some uncertainty remains in predic t- ing the boron concentration above which metallic conduc- tion takes place [17], [18], [19], [20], [21].
The isothermal bulk modulus B (and the compress- ibility , 1/ B ) can be used as a quantitative character- istic describing relations between the structure and atomic forces, from one side and the physical properties of solids, from another side. Dubrovinskaia et al. [22] reported the results of high pressure-high temperature synthesis of bo- ron-doped diamond and the results of experimental deter- mination of its bulk modulus. In addition, they proceeded to detailed a theoretical calculation which suggested very little (within computational uncertainty) effect of the dop- ing on the compressibility of diamond for impurity concen- trations up to 3 at %. These calculations also confirmed that boron atoms prefer to substitute C-atoms in a diamond
structure. It is the aim of this short paper to draw attention
Vassiliki Katsika-Tsigourakou
Department of Solid State Physics, Faculty of Physics, University of Atens, Panepistimiopolis, 157 84 Zografos, Greece
E-mail- vkatsik@ph ys.uoa.gr
to the following point: Instead of the aforementioned tedi- ous theoretical calculation, a simple thermodynamical model can be alternatively used for the estimation of the
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 3, Issue 3, March-2012 2
ISSN 2229-5518
boron-concentration dependence of the compressibility of diamond. This thermodynamical model, has been original-
gi ci B where B stands, as mentioned, for the isother- mal bulk modulus ( 1 / ) , the mean volume per atom
ly suggested for the formation and/or migration processes
and ci
is dimensionless quantity. (The superscript i refers
of defects in solids [23], [24], [25] and has been successfully
applied in a large variety of solids (including the case of
noble gas solids [26]), that have been reviewed in [27] and
[28]. The same model was extended [27] to describe the
to the defect process under consideration, e.g. defect forma- tion, defect migration and self-diffusion activation). By dif- ferentiating this relation in respect to pressure P , we find
the defect volume i [ ( i ) ]
dg dP T
. The compressibility
physical properties of the electric signals that precede rup-
ture [29]. In the next section, we recapitulate this model
d ,i
defined by
d ,i [ (d ni
dP)T ]
, is given by:
(termed cB model, see below) and then in section 3 we


d ,i (1 B) (d 2 B dP2 ) [(dB dP)
1]
(4)
apply it to the case of the compressibility of boron-doped
This relation states that the compressibility
d ,i
does not
diamond. We note that the success of this model to repro- duce the self-diffusion coefficients of diamond has been
depend on the type i of the defect process. Thus, it seems
reasonable to assume [32], [27] that the validity of (4) holds
already checked in [30].
also for the compressibility d
involved in (2), i.e.,



d 2 2
1 (d B1
dP ) [(dB1
dP)T 1]
(5)
2 THE MODEL
where the subscript <1> in the quantities at the right side denotes that they refer to the undoped diamond crystal.
Let us denote V1
and V2
the corresponding molar volumes,
i.e. V1 N1 and V2 N2
(where N stands for Avogadro’s
3 APPLICATION OF THE MODEL TO THE BO-
number) for diamond (density 3.51 gr/cm3) and B4C (den-
sity 2.48 gr/cm3) respectively. Defining a “defect volume”
RON-DOPED DIAMOND
[31]


d as the variation of the volume V , if one “mole- 2 2
1 In general, the quantities
dB1
dP and
d B1
dP , can be
cule” of type “1” is replaced by one “molecule” of type “2”,
it is evident that the addition of one “molecule” of type “2”
roughly estimated from the modified Born model accord- ing to [27], [31]:


to a crystal containing N “molecules” of type “1” will in- B


2 2 B
dB1
d d
dP (n
7) 3 and B1 (d B1
dP ) (4 9)(n
3)
(6)
crease its volume by
1 . Assuming that
is inde-
where nB
is the usual Born exponent. In cases, however,
pendent of composition, the volume VN n
of a crystal con-
where the Born model does not provide an adequate de-
taining N “molecules” of type (1) and n “molecules” of
type “2” can be written as [27], [28], [29], [30], [31]:

d
scription, we can solely rely on (4), but not on (6). In other words, if Born model holds, we calculate the first and sec-
VN n [1 (n N )]V1 n
(1)
ond pressure derivatives of the bulk modulus on the basis
The compressibility of the doped diamond can be found by differentiating (1) with respect to pressure which finally gives [27]:

d d
of (6) and then insert them into (4). Otherwise, we insert
into (4) the first and second pressure derivative of the bulk
modulus deduced from the elastic data under pressure (ob-
tained either from laboratory measurements or from micro-
1 1 1 1
VN n V n N
N
V (2)
where d
denotes the compressibility of the volume d ,
scopic calculations) using a least squares fit to a second or-
der Murnaghan equation. The results of these possibilities
defined as [32]


d (1 d ) (dd
dP)T .
are now described below for the boron-doped diamond.
Within the approximation of the hard-spheres model, the
“defect-volume” d can be estimated from:
We shall use hereafter the experimental value
B1 =442 GPa

d (V V ) N
(3)
obtained in Refs [8], [22], [33] for the pure diamond crystal.
In Dubrovinskaia et al. [22], the experimental pres-
Thus, if VN n
can be determined from (1) (upon either
sure-volume data were fitted using the third order Birch-
considering (3) or other type of measurements and/or
Murnaghan equation of state. This fitting procedure for
method), the compressibility can be found from (2) if a
(undopted) diamond gave
B1 =442(4) GPa,
B =3.2(2) –
procedure for the estimation of
d will be employed. In
this direction, we adopt a thermodynamical model, termed
where B1
denotes the first pressure derivative of
B1 - and
cB model, for the formation and migration of the defects
in solids [23], [24], [25], [26], [27], [28]. According to this
i
the zero- pressure volume 3.4157(9) cm3/mol which within
the uncertainty coincide with the data from [8]. For boron-
doped diamond, at the doping level of 2.6 at % they found
model, the defect Gibbs energy
g is interconnected with
the bulk properties of the solid through the relation
B =436(7) GPa, B =3.1(2) and the zero- pressure volume
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 3, Issue 3, March-2012 3
ISSN 2229-5518
3.4319(9) cm3/mol.
Using the aforementioned values for the zero-
pressure volume of the undoped and the boron-doped di-
amond we determined d
on the basis of (1). Let us now
investigate the
( 1 / B)
value resulting from (2) at the
doping level of 2.6 at % when employing the determination
of the above:
d -value by means of the procedures described
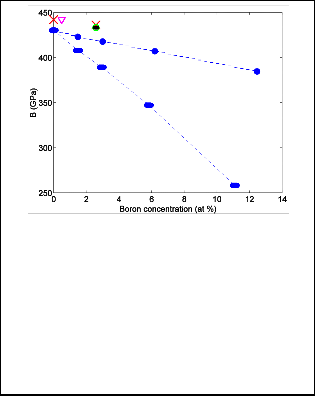
First, when employing the modified Born model –and hence use (6)- we find B 433 GPa. This is marked with open circle in Fig. 1 and is very close to the experimental value B =436(7) GPa measured in [22] (marked with cross in Fig. 1).
Second, we now employ the Morse potential parameters determined –in the frame of an analytic mean field ap- proach- by fitting the compression experimental data of diamond at ambient temperature. For example see Fig. 3 of
Fig. 1. Dependence of the isothermal bulk modulus on the boron concentration. Experimental values obtained in [22], [33] are shown with crosses. Calculated results of the bulk moduli with substitutional (solid circles) and interstitials (squares) boron impurities according to [22], [33]. The results calculated in this paper are designated with open circles and open squares when employing (2) and using the compr essibil-
[34] which, if described by an expansion of the isothermal
ity d
of the defect volume obtained either from the modified
bulk modulus carried out to second order, gives
B =3.3
Born model or from the analytic equation of state in [34] de-
scribed in the text. The latter calculation was repeated by considering, instead of 2.6 at %, the more recent value 0.5 at
and
B =-0.0024 GPa-1. By inserting these
and
val-
% reported in [35], and led to the value B =441.9 GPa
ues into (5) we find d
and then from (2) we get B =433
shown by the inverted triangle.
GPa (marked with open square in Fig. 1). This is also very close to the experimental value B =436(7) GPa reported in [22]. Finally, we note that the latter calculation was repeat- ed by using, instead of the aforementioned doping level 2.6 at %, the value of 0.5 at % that was later reported [35] as being more representative of the reality since it was de- duced after closer investigations of the microstructure of
4 CONCLUSION
To summarize, for boron-doped diamond, at doping level of 2.6 %, Dubrovinskaia et al [22] reported the experimental value of the isothermal bulk modulus B =436 GPa. The val-
boron-doped diamond and of boron distribution. This led
ues of
B( 1 / )
calculated here on the basis of (2) are
to the calculated value B =441.9 GPa marked with an in-
found to be 433 GPa when using the
d -value obtained
verted triangle in Fig. 1, which also agrees with the exper-
imental results, if the experimental error is considered.
from (4) in terms of
and
B , of (undoped) diamond
estimated from the either modified Born model or its ana-
lytic equation of state based on an analytic mean field ap-
proach. In view of a large error in the boron- content, the position of this experimental point in Fig. 1 can be found
[33] at a concentration as low as 2 at %. In this case the cal- culated B -values from (2) are found to be around 435 GPa, thus being again in very good agreement with the experi- mental value [22] of 436 GPa. Finally, if we alternatively use an even lower concentration of 0.5 at %, which was lat- er [35] reported as being closer to the reality, our calculated value is around 441.9 GPa which also agrees with the ex- perimental results, if the experimental uncertainty is con- sidered. For the sake of comparison, we note that the calcu- lated B -value in the framework of the density functional method [33] is around 421 GPa.
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 3, Issue 3, March-2012 4
ISSN 2229-5518
REFERENCES
[1] A.K. Pandey, N. Alam and A. Kumar, International Journal of Scientific
& Engineering Research, vol. 3, iss. 4, April 2012.
[2] S. Fahy and S.G. Louie, Phys. Rev. B, vol. 36, pp. 3373, 1987.
[3] S.J. Clark and C.J. Ackland, J. Crain, Phys. Rev. B, vol. 52, pp. 15035,
1995.
[4] M. Hanfland, K. Syassen, S. Fahy, S.G. Louie and M.L. C ohen, Phys.
Rev. B, vol. 31, pp. 6896, 1985.
[5] H.K. Mao and R.J. Hemley, Nature, vol. 351, pp. 721, 1991.
[6] S. Sera, G. Benedek and L. Miglio, Phys. Rev. B, vol. 57, pp. 5661, 1998.
[7] R. Maezono, A. Ma, M. D. Towler and R. J. Needs, Phys. Rev. Lett.,
Vol. 98, pp. 025701, 2007.
[8] F. Occelli, P. Loubeyre and R. LeToullec, Nat. Matters, vol. 2, pp. 151,
2003.
[9] P.h. Gillet, G. Fiquet, I. Daniel, B. Reynard and M. Hanfland, Phys.
Rev. B, vol. 60, pp. 14660, 1999.
[10] E.S. Zouboulis, M. Grimsditch, A.K. Ramdas and S. Rodr iguez, Phys.
Rev. B, vol. 57, pp. 2889, 1998.
[11] N. Mounet and N. Marzari, Phys. Rev. B, vol. 71, pp. 205214, 2005.
[12] Agnes Dewaele, Frederic Datchi, Paul Loubeyre and Mohamed
Mezouar, Phys. Rev. B, vol. 77, pp. 094106, 2008.
[13] M.H. Grimsditch and A.K. Ramdas, Phys. Rev. B, vol. 11, pp. 3139,
1975.
[14] R. Vogelgesang, A.K. Ramdas, S. Rodriguez, M. Grimsditch and T.R.
Anthony, Phys. Rev. B, vol. 54, pp. 3989, 1996.
[15] H.K. Mao and R.J. Hemley, Nature (London), vol. 351, pp. 721, 1991. [16] Y. Haitao, Y. Haixue and R.B. Jackman, Semicond. Sci. Technol., vol. 20,
pp. 296, 2005.
[17] T. Tshepe, C. Kasl. J. Prins and M.J.R. Hoch, Phys. Rev. B: Condens.
Matter, vol. 70, pp. 245107, 2004.
[18] L. Boeri, J. Kortus and O.K. Anderson, Phys. Rev. Lett., vol. 93, pp.
237002, 2004.
[19] E.A. Ekimov, V.A. Sidorov, E.D. Bauer, et al., Nature (Lon-don), Vol.
428, pp. 542, 2004; V.A. Sidorov, E.A. Ekimov, S.M. Stishov, et al.,
Phys. Rev. B: Condens. Matter, vol. 71, pp. 060502(R), 2005.
[20] J. Nakamura, E. Kabasawa, N. Yamada, et al., Phys. Rev. B: Condens.
Matter, vol. 70, pp. 245111, 2004.
[21] T. Yokoya, T. Nakamura, T. Matsushita, et al., Nature (London), Vol.
438, pp. 647, 2005.
[22] N. Dubrovinskaia, L. Dubrovinsky, W.A. Crichton, E. Zarechnaya, E.I. Isaev and I.A. Abrikosov, High Pressure Research, vol. 26, pp. 79,
2006.
[23] P. Varotsos, Phys. Rev. B, vol. 13, pp. 938, 1976; J. Physique (France)
Lettr.,vol. 38, pp. L455, 1977; Phys. Status Solidi B, vol. 90, pp. 339,
1978 ; Phys. Status Solidi B, vol. 100, pp. K133, 1980.
[24] P. Varotsos and K. Alexopoulos, Phys.Rev. B, vol. 15, pp. 4111, 1977;
vol. 15, pp. 2348, 1977 ; vol. 21, pp. 4898, 1980; vol. 24, pp. 904, 1981;
vol. 24, pp. 3606, 1981.
[25] P. Varotsos and K. Alexopoulos, J. Phys. Chem. Solids, vol. 39, pp. 759,
1978; J. Phys. C: Solid State, vol. 12, pp. L761, 1979; Phys. Status Solidi
A, vol. 47, pp. K133, 1978; Phys.Rev. B, vol. 22, pp. 3130, 1980.
[26] P. Varotsos and K. Alexopoulos, Phys.Rev. B, vol. 30, pp.7305, 1984.
[27] P. Varotsos and K. Alexopoulos, Thermodynamics of Point Defects and
Their Relation With the Bulk Properties, North-Holland, Amsterdam,
1986.
[28] P. Varotsos, J. Appl. Phys., vol. 101, pp. 123503, 2007; Solid State Ionics,
vol. 179, pp. 438, 2008.
[29] P. Varotsos and K. Alexopoulos, Tectonophysics, vol. 110, pp. 73, 1984; vol.110, pp. 99, 1984; vol. 188, pp. 321, 1991; vol. 224, pp. 269, 1993; vol. 224, pp. 1, 1993; P. Varotsos, K. Alexopoulos, K. Nomicos et al., Nature (London),vol. 322, pp. 120, 1986; P.A. Varotsos, N.Sarlis and
E.S. Skordas, Phys. Rev. E, vol. 66, pp. 011902, 2002; vol. 67, pp.
021109, 2003; vol. 68, pp. 031106, 2003; S. Abe, N. Sarlis, E.S. Skordas
et al. Phys. Rev. Lett., vol. 94, pp. 170601, 2005.
[30] P. Varotsos, Phys.Rev. B, vol. 75, pp. 172107, 2007.
[31] P. Varotsos, Phys. Status Solidi B, vol. 99, pp. K93, 1980; J. Phys. Chem.
Solids, vol. 42, pp. 405, 1981; P. Varotsos and K. Alexopoulos, J. Phys. Chem. Solids, vol. 41, pp. 1291,1980.
[32] P. Varotsos, W. Ludwig and K. Alexopoulos, Phys. Rev. B, vol. 18, pp.
2683, 1978; P. Varotsos and W. Ludwig, J. Phys C: Solid State, vol. 11, pp. L305, 1978.
[33] E.Yu. Zarechnaya, E.I. Isaev, S.I. Simak, Yu.Kh. Vekilov, L.S.
Dubrovinsky, N.A. Dubrovinskaia and I.A. Abrikosov, Journal of Ex- perimental and The oretical Physics, vol. 106, pp. 781, 2008.
[34] Y. Wei, J.X. Sun and R.G. Tian, Diamond and Related Materials, Vol. 18, pp. 632, 2009.
[35] N. Dubrovinskaia, R. Wirth, J. Wosnitza, T. Papageorgiou, H.F.
Braun, N. Miyajima and L. Dubrovinsky, Proc. Natl. Acad. Sci. USA, vol. 105, pp. 11619-11622, 2008.
IJSER © 2012
http://www.ijser.org