International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 1

ISSN 2229-5518

A Proposed Solution for Sorting Algorithms Problems by Comparison Network Model of Computation.

Mr. Rajeev Singh, Mr. Ashish Kumar Tripathi, Mr. Saurabh Upadhyay, Mr.Sachin Kumar Dhar Dwivedi

Abstract:-In this paper we have proposed a new solution for sorting algorithms. In the beginning of the sorting algorithm for serial computers (Random access machines, or RAM’S) that allow only one operation to be executed at a time. We have investigated sorting algorithm based on a comparison network model of computation, in which many comparison operation can be performed simultaneously.

Index Terms

Sorting algorithms, comparison network, sorting network, the zero one principle, bitonic sorting network

1 Introduction

There are many algorithms for solving sorting algorithms (networks).A sorting network is an abstract mathematical model of a network of wires and comparator modules that is used to sort a sequence of numbers. Each comparator connects two wires and sorts the values by outputting the smaller value to one wire and the large to the other. A sorting network consists of two items comparators and wires .each wires carries with its values and each comparator takes two wires as input and output. This independence of comparison sequences is useful for parallel execution of the algorithms. Despite the simplicity of the model, sorting network theory is surprisingly deep and complex.

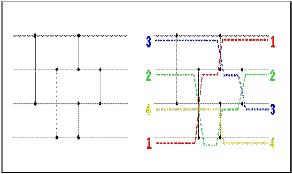
A sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order Efficient sorting is important for optimizing the use of other algorithms that require sorted lists to work correctly; it is also often useful for data and for producing human-readable output. More formally, the output must satisfy two conditions:
1.1 The output is in no decreasing order (each element is no smaller than the previous element according to the
desired total order);

1.2 The output is a permutation, or reordering, of the input.

For example of bubble sort 8, 25,9,3,6

8 8 8 3 3

25 25 9 9 3 8 6 6

9 25 3 9 6 8

3	25	6	9
6		25

We can easily construct a network of any size recursively using the principles of insertion and selection. Assuming we have a sorting network of size n, we can construct a network of size n +

1 by "inserting" an additional number into the already sorted subnet . We can also accomplish the same thing by first "selecting" the lowest value from the inputs and then sort the remaining values recursively (using the principle behind bubble sort).

5 n n

n+1

International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 2

ISSN 2229-5518

A Sorting Network constructed recursively that first sinks the largest value of the bottom and then sorts the remaining wires. Based on bubble sort.

5 n- n

n+1

A Sorting Network constructed recursively that first sort the first n wires and then sorts the remaining wires. Based on Insertion sort.
The structure of these two sorting networks is very similar. A
construction of the two different variants, which collapses together comparators that can be performed simultaneously shows that, in fact, they are identical

Bubble sorting network

Insertion Sorting Network.

2 Comparator network

A sorting network consists of two items: comparators and wires. Each wire carries with it a value, and each comparator takes two wires as input and output. When two values enter a comparator, the comparator emits the lower value from the top wire, and the higher value from the bottom wire. A network of wires and comparators that will correctly sort all possible inputs into ascending order is called a sorting network.

X min(x,y)

Comparator

Y max(x,y)
A Comparator is a mapping {I,j} An → An ,I, j ∑ {0--------n-1} min(X,Y)
With
{i, j) (a) I = min (ai, aj)
max(X,Y)
{i,j} (a) j=max (ai, aj),
{I,j} (a) k = ak for all k with k ≠ I, k ≠ j
For all a £ An

3 Objectives

To present that is one after all operations in a comparison network may occur at the same time or “in parallel” We investigate sorting algorithm based on a comparison network model of computation, in which many comparison operations can be performed simultaneously.

4 The zero-one principle

The zero one principle says that if a sorting networks work
correctly when each input is drawn from the set {0,1}.then it works correctly an arbitrary input numbers. The numbers can be integers, reals or in general, any set of values from any linearly ordered set. as we construct sorting network and other comparison networks the zero one principle will allow us to focus on their operation for input sequence consisting solely of 0’s and
1’s.it is easy to prove the validity of some sorting networks (like the insertion sort, bubble sort),it is not always so easy. There are n permutations of numbers in an n-wire network, and to test all of them would take a significant amount of time, especially when n is large. The number of test cases can be reduced significantly, to 2n, using the so called zero-one principle. the zero one principle states that a sorting networks is valid if it can sort all 2n sequence of 0’s and 1’s.
If a comparison network transforms the input sequence
a={a1,a2,….an} into the output sequence b={b1,b2,….bn} then for any monotonically increasing function f,the network transforms the input sequence f(a) =<f(a1),f(a2),……….f(an)> into the output sequence f(b)= <f(b1),f(b2),………f(bn)>.

5 Bitonic sorters

The first steps in our construction of an efficient sorting network
is to construct a comparison network that can sort any bitonic

International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 3

ISSN 2229-5518

sequence, a sequence that monotonically increase and monotonically decrease or can be circularly shifted to become monotonically increasing and then monotonically decreasing.
For example, the sequences <1,4,6,8,3,2>,<6,9,4,2,3,5> and
<9,8,3,2,4,6> are all bitonic. The bitonic sorter that we shall construct is a comparison network that sorts bitonic sequence of
0’s and 1’s.for example 0000----------111--------0000…………

For example 1, 3,9,22,56,98,95,2511,4,2

Eg 00011000

If no of 0’s > no of 1’s then in upper half all zero’s and in lower half a bitonic sequence, if no of 1’s>no of 0’s then lower half completely 1’s and upper half a bitonic sequence, if no of 1’s = no of 0’s upper half all zero & lower half all 1’s.no of comparator used in bitonic sorter = nlogn. Complexity of bitonic sequence
=0(log2n), where n = no of I/P.
A bitonic sorter is composed of several stages, each of which is
called half cleaner, each half cleaner is a comparison network of depth 1 in which input line I is composed with line i+n/2 for i-
1,2,…………….n/2.sort the sequence 18,22,56,98,102,88,76,24
using bitonic is complexity log2n
Merging network:(V)-our sorting network will be constructed from merging will be constructed from merging networks, which are networks that can merge two sorted input sequence into one sorted input sequence .we modify bitonic sorter[n] to create the merging network merger [n].
For example, given the sorted zero one sequence
X=000000000111
Y=000000001111, we reverse y to get yR 111100000000
Concatenating X and yR yields. Thus to merge the two input sequence X and Y, it suffices to perform a bitonic sort on x concatenated with yR.
For example s1: 18, 25, 96, 102, and 105,

s2:7, 43, 98 merging of two sorted sequence using bitonic method.

18 7

25 18

96 25

102 43

105 96

98 98

7 105

6 Analysis of sorting network

Can sort any input sequence. The sorting network sorter[n] uses the merging network to implement a parallel version of merge
The depth d(n)of sorter [n]is the depth log2n of merger [n] consequently, the depth of sorter[n] is given by the recurrence. D[n] = 0 if n=1
D (n/2) +logn if n=2k and k>=1
We can sort n numbers in parallel in (log2 n) time.
Counting sort cannot be implemented on a comparison network.

7CONCLUSION

Thus an algorithm such as counting sort cannot be implemented on a comparison network. Second the RAM model in which operations occur serially that is one after another operations in a comparison network may occur at the same time or in parallel”. As we shall see, this characteristic allows the construction of comparison network that sort n values in sub linear time.

8 References

1Improved Algorithms and analysis for secretary problems and generalizations. In proceeding of the 36 th annual Symposium on foundation of computer science.

International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 4

ISSN 2229-5518

2 Mohammad Akra and Louay Bazzi: on the solution of linear recurrence equations.computional optimization and applications.
3. G.M Adel’s on-vel’skii and E.M Landis.An algorithm for the organization of information .sovier mathematics doklady.
4. Eric Bach and Jeffery Shallit.algorithmic number theory- volume-I: Efficient algorithms, The MIT press, 1996
5 R.Bayer and E.M McCreight.Organization and maintenance of
large ordered indexes.Acta Information 1(3):173-189, 1972.
6. Pierre Beauchemin, Gilles Brassard, and Claude Creapeau and
Carl Pomerance.The generation of random numbers that is probably prime.
7. Yinyu Ye.Interior Point Algorithms: Theory and analysis, john wikley $Sons, 1997
8. JeanVuillemin.Adata structure for manipulating priority queues.coomunication of the ACM.
9. Mark Allen Weise.Data Structures and Problems Solving
Using Java.
10. C.A.R .Hoare .Merge sort. Computer Journal, 5(!): 10-15,
1962
11. O. Angel, A.E. Holroyd, D. Romik, B. Virag, Random

Sorting Network Adv. in Math., 215(2):839–868, 2007.

12. K.E.Batcher, sorting network and their application
Proceedings of the AFIPS Spring Joint Computer Conference 32,
307–314 (1968).
13. D.E. Knuth the, Volume 3: Sorting and Searching, Third
Edition. Addison-Wesley, 1997.ISBN 0-201-89685-0 Section
5.3.4: Networks for Sorting, pp. 219–247.
14.Ajtai, M.; Komlós, J.; Szemerédi, E. (1983), "An O(n log n) sorting network", Proceedings of the 15th Annual ACM Symposium on Theory .
15. M. S. Paterson, Improved sorting networks with

O(log N) depth, Algorithmica 5 (1990), no. 1, pp. 75–

92, doi:10.1007/BF01840378.
16. M. Mitchell, an Introduction to Genetic Algorithms, the MIT Press, 1998.ISBN-0-262-63185-7. Chapter 1: Overview, pp. 21–
27

Author:-

1 Mr. Rajeev Singh is currently working in Dept. of CS, Centre
for Management Technology Greater Noida, U.P, India
E-mail:-rajeevsisodiamca@gmail.com
2 Mr. Ashish Kumar Tripathi is currently working in Dept. of CS, Centre for Management Technology Greater Noida, U.P, India
E-mail:-ashish.msa@gmail.com
3 Mr.Saurabh Upadhyay is currently working in Dept. of CS, S.M.S Varanasi, U.P, INDIA
E-mail:- saurabhupad@gmail.com
4Mr.Sachin Kumar Dhar Dwivedi, Assistant Engineer National

Institute of Electronics and Information Technology, Aizawl, India.

E-mail:-sachin8071@gmail.com